题目内容
11．满足{0，1}⊆P⊆{0，1，2，3，4，5}的集合P的个数是16．分析 易知0，1∈P，2，3，4，5可在或不在集合P中，从而求P的个数．
解答 解：∵{0，1}⊆P⊆{0，1，2，3，4，5}，
∴0，1∈P，2，3，4，5可在或不在集合P中，
∴集合P的个数是24=16，
故答案为：16．
点评 本题考查了集合的化简与集合的子集的个数的应用．
练习册系列答案
相关题目
2．命题p：关于x的不等式（x-2）$\sqrt{{x}^{2}-3x+2}$≥0的解集为{x|x≥2}，命题q：若函数y=kx2-kx-1的值恒小于0，则-4＜k≤0，那么不正确的是（ ）
| A． | “非p”为假命题 | B． | “非q”为假命题 | C． | “p或q”为真命题 | D． | “p且q”为假命题 |
16．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≥3}\\{f（x+1），x＜3}\end{array}\right.$，则f（1+log23）的值为（ ）
| A． | $\frac{1}{24}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
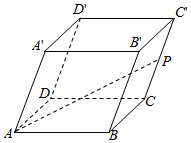在平行六面体ABCD-A′B′C′D′中，AB=4，AD=6，AA′=8，∠BAD=90°，∠BAA′=∠DAA′=60°，P是CC1的中点．