题目内容
15.已知关于x的方程x2+zx+1+2i=0有实根,则复数z的模的最小值为$\sqrt{2\sqrt{5}+2}$.分析 设x=x0是方程x2+zx+1+2i=0的实数根,可求得z=-x0-$\frac{1}{{x}_{0}}$-$\frac{2}{{x}_{0}}$i,继而可得其模的解析式,应用基本不等式即可求得答案.
解答 解:设x=x0是方程x2+zx+1+2i=0的实数根,
则${{x}_{0}}^{2}$+zx0+1+2i=0,
即z=-x0-$\frac{1}{{x}_{0}}$-$\frac{2}{{x}_{0}}$i,
|z|=$\sqrt{{({-x}_{0}-\frac{1}{{x}_{0}})}^{2}{+(\frac{2}{{x}_{0}})}^{2}}$=$\sqrt{{{x}_{0}}^{2}+\frac{5}{{{x}_{0}}^{2}}+2}$≥$\sqrt{2\sqrt{5}+2}$,
当且仅当x0=±$\root{4}{5}$时,等号成立.
∴|z|的最小值为:$\sqrt{2\sqrt{5}+2}$,
故答案为:$\sqrt{2\sqrt{5}+2}$.
点评 本题考查复数代数形式的混合运算,考查复数模的应用,熟练应用基本不等式是求|z|的最小值的关键,属于中档题.

练习册系列答案
相关题目
7.A={x|x>0},B={x|x2-1<0},A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x>1} | C. | {x|x>0} | D. | {x|0<x<1} |
4.在平行四边形ABCD中,AB=2,BC=1,∠ABC=120°,平面ABCD内有一点P,满足AP=$\sqrt{5}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$(λ,μ∈R),则2λ+μ的最大值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{15}}{3}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{\sqrt{15}}{6}$ |
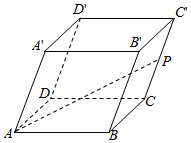 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.