题目内容
18.若函数$f(x)=a-\frac{b}{{{2^x}+1}}(a,b为常数)$是奇函数,则a,b的一组可能值为( )| A. | a=1,b=2 | B. | a=2,b=1 | C. | a=-1,b=2 | D. | a=2,b=-1 |
分析 可看出f(x)的定义域为R,从而可知f(x)为R上的奇函数,从而有f(0)=$a-\frac{b}{2}$=0,这样只需验证每个选项的a,b值是否满足该式便可找出正确选项.
解答 解:f(x)为R上的奇函数;
∴f(0)=0;
即$a-\frac{b}{2}=0$;
可看出,a=1,b=2时满足上式;
即a=1,b=2为a,b的一组可能值.
故选A.
点评 考查奇函数的概念,指数函数的值域,函数定义域的求法,以及奇函数在原点有定义时,原点处的函数值为0.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.将函数y=sin(x-$\frac{π}{6}$)的图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$倍(纵坐标不变),再将所得函数的图象向左平移$\frac{π}{6}$个单位,最后所得到的图象对应的解析式是( )
| A. | y=sin$\frac{1}{2}$x | B. | y=sin($\frac{1}{2}$x-$\frac{π}{6}$) | C. | y=sin2x | D. | y=sin(2x+$\frac{π}{6}$) |
7.A={x|x>0},B={x|x2-1<0},A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x>1} | C. | {x|x>0} | D. | {x|0<x<1} |
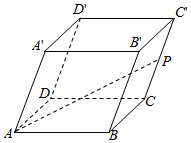 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.