题目内容
13.函数y=$\sqrt{4-{x}^{2}}$的定义域是( )| A. | (-2,2) | B. | [-2,2] | C. | (-∞,-2) | D. | (2,+∞) |
分析 直接由根式内部的代数式大于等于0求得x的取值范围得答案.
解答 解:由4-x2≥0,解得-2≤x≤2.
∴函数y=$\sqrt{4-{x}^{2}}$的定义域是[-2,2].
故选:B.
点评 本题考查函数的定义域及其求法,考查一元二次不等式的解法,是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
4.在平行四边形ABCD中,AB=2,BC=1,∠ABC=120°,平面ABCD内有一点P,满足AP=$\sqrt{5}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$(λ,μ∈R),则2λ+μ的最大值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{15}}{3}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{\sqrt{15}}{6}$ |
9.下列命题中,正确的是( )
| A. | 若z是复数,则|z|2=z2 | |
| B. | 任意两个复数不能比较大小 | |
| C. | 当b2-4ac>0时,一元二次方程ax2+bx+c=0(a、b、c∈C)有两个不相等的实数根 | |
| D. | 在复平面xOy上,复数z=m2+mi(m∈R,i是虚数单位)对应的点的轨迹方程是y2=x |
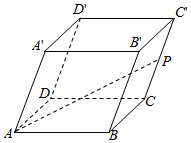 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.