题目内容
现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图1).在直角坐标平面内,我们定义A(x1,y1),B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
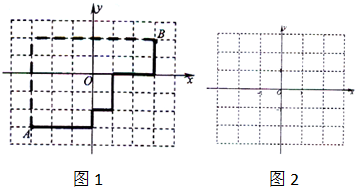
(1)已知A(-3,-3),B(3,2),求A、B两点的距离D(AB).
(2)求到定点M(1,2)的“直角距离”为2的点的轨迹方程.并写出所有满足条件的“格点”的坐标(格点是指横、纵坐标均为整数的点).
(3)求到两定点F1、F2的“直角距离”和为定值2a(a>0)的动点轨迹方程,并在直角坐标系如图2内作出该动点的轨迹.
①F1(-1,0),F2(1,0),a=2;
②F1(-1,-1),F2(1,1),a=2;
③F1(-1,-1),F2(1,1),a=4.

(1)已知A(-3,-3),B(3,2),求A、B两点的距离D(AB).
(2)求到定点M(1,2)的“直角距离”为2的点的轨迹方程.并写出所有满足条件的“格点”的坐标(格点是指横、纵坐标均为整数的点).
(3)求到两定点F1、F2的“直角距离”和为定值2a(a>0)的动点轨迹方程,并在直角坐标系如图2内作出该动点的轨迹.
①F1(-1,0),F2(1,0),a=2;
②F1(-1,-1),F2(1,1),a=2;
③F1(-1,-1),F2(1,1),a=4.
考点:轨迹方程
专题:综合题,新定义
分析:(1)直接由直角距离的概念求解;
(2)由定义写出轨迹方程,然后找满足条件的整数数对得到格点数;
(3)由定义写出轨迹方程,分类讨论去绝对值后即可作出图象.
(2)由定义写出轨迹方程,然后找满足条件的整数数对得到格点数;
(3)由定义写出轨迹方程,分类讨论去绝对值后即可作出图象.
解答:
解:(1)∵A(-3,-3),B(3,2),
∴D(AB)=|x1-x2|+|y1-y2|=|-3-3|+|-3-2|=11;
(2)由题意可知轨迹方程为:|x-1|+|y-2|=2.
满足条件的格点为:(1,4),(1,0),(2,3),(2,1),(3,2),
(0,1),(0,3),(-1,2);
(3)①F1(-1,0),F2(1,0),a=2.
轨迹方程为:|x+1|+|x-1|+2|y|=4.
当x≤-1,y≥0时,x-y+2=0.
当x≤-1,y<0时,x+y+2=0.
当-1<x<1,y≥0时,y=1.
当-1<x<1,y<0时,y=-1.
当x≥1,y≥0时,x+y-2=0.
当x≥1,y<0时,x-y-2=0.

②F1(-1,-1),F2(1,1),a=2.
轨迹方程为:|x+1|+|y+1|+|x-1|+|y-1|=4.
当x≤-1,y≥1时,(x,y)=(-1,1).
当x≤-1,-1<y<1时,x=-1.
当x≤-1,y≤-1时,(x,y)=(-1,-1).
当-1<x<1,y≥1时,y=1.
由对称性可得其它几种情况.

③F1(-1,-1),F2(1,1),a=4.
迹方程为:|x+1|+|y+1|+|x-1|+|y-1|=8.
当x≤-1,y≥1时,x-y+4=0.
当x≤-1,-1<y<1时,x=-3.
当-1<x<1,y≥1时,y=3.
由对称性可得其它几种情况.

∴D(AB)=|x1-x2|+|y1-y2|=|-3-3|+|-3-2|=11;
(2)由题意可知轨迹方程为:|x-1|+|y-2|=2.
满足条件的格点为:(1,4),(1,0),(2,3),(2,1),(3,2),
(0,1),(0,3),(-1,2);
(3)①F1(-1,0),F2(1,0),a=2.
轨迹方程为:|x+1|+|x-1|+2|y|=4.
当x≤-1,y≥0时,x-y+2=0.
当x≤-1,y<0时,x+y+2=0.
当-1<x<1,y≥0时,y=1.
当-1<x<1,y<0时,y=-1.
当x≥1,y≥0时,x+y-2=0.
当x≥1,y<0时,x-y-2=0.

②F1(-1,-1),F2(1,1),a=2.
轨迹方程为:|x+1|+|y+1|+|x-1|+|y-1|=4.
当x≤-1,y≥1时,(x,y)=(-1,1).
当x≤-1,-1<y<1时,x=-1.
当x≤-1,y≤-1时,(x,y)=(-1,-1).
当-1<x<1,y≥1时,y=1.
由对称性可得其它几种情况.

③F1(-1,-1),F2(1,1),a=4.
迹方程为:|x+1|+|y+1|+|x-1|+|y-1|=8.
当x≤-1,y≥1时,x-y+4=0.
当x≤-1,-1<y<1时,x=-3.
当-1<x<1,y≥1时,y=3.
由对称性可得其它几种情况.

点评:本题是新定义题,考查了分类讨论的数学思想方法,关键是对题意的理解,是中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
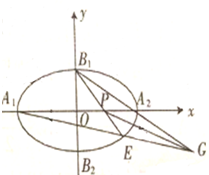 已知焦点在x轴上的椭圆C的短轴长为2,离心率为
已知焦点在x轴上的椭圆C的短轴长为2,离心率为