Question

已知焦点在x轴上的椭圆C的短轴长为2，离心率为

3

2

．
（1）求椭圆C的标准方程；
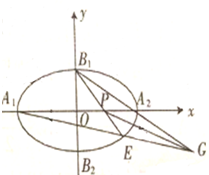
（2）如图所示，A₁，A₂，B₁，B₂是椭圆C的顶点，E是椭圆上任意一点（顶点除外）B₁E交x轴于点P，直线A₂B₁交A₁E于点G，设直线A₁E的斜率为k₁，直线GP的斜率为k₂，证明k₁-2k₂为定值，并求出这个定值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：计算题,圆锥曲线中的最值与范围问题

分析：（1）由题意得

2b=2 c a = 3 2 a2=b2+c2

，从而求出a=2，b=1，c=

3

；从而写出椭圆方程；
（2）可设直线A₁E的方程为y=k₁（x+2）；从而求出E（-

8 k 2 1 -2

4 k 2 1 +1

，

1

4 k 2 1 +1

4

k

1

），再由直线A₂B₁与直线A₁E方程联立求出点G（

2-4k1

2k1+1

，

4k1

2k1+1

），再由B₁（0，1），E（-

8 k 2 1 -2

4 k 2 1 +1

，

1

4 k 2 1 +1

4

k

1

），P（x，0）共线求点P（-

4k1+2

2k1-1

，0），从而表示出PG的斜率k₂，从而求k₁-2k₂是定值．

解答： 解：（1）由题意，

2b=2 c a = 3 2 a2=b2+c2

，
解得，a=2，b=1，c=

3

；
故椭圆C的标准方程为

x2

4

+y²=1；
（2）证明：∵A₁（-2，0），E是椭圆上任意一点（顶点除外），
则可设直线A₁E的方程为y=k₁（x+2）；
联立

y=k1(x+2) x2 4 +y2=1

得，
（4k²₁+1）x²+16k²₁x+16k²₁-4=0；
x_E-2=-

16 k 2 1

4k21+1

；x_E=-

8 k 2 1 -2

4 k 2 1 +1

；
y_E=k₁（-

8 k 2 1 -2

4 k 2 1 +1

+2）=

1

4 k 2 1 +1

4

k

1

；
故E（-

8 k 2 1 -2

4 k 2 1 +1

，

1

4 k 2 1 +1

4

k

1

）；
又直线A₂B₁的方程为y=-

1

2

x+1；
联立

y=k1(x+2) y=- 1 2 x+1

解得G（

2-4k1

2k1+1

，

4k1

2k1+1

），
由B₁（0，1），E（-

8 k 2 1 -2

4 k 2 1 +1

，

1

4 k 2 1 +1

4

k

1

），P（x，0）共线得，
x=-

4k1+2

2k1-1

，故P（-

4k1+2

2k1-1

，0）；
所以PG的斜率k₂=

4k1 2k1+1 -0

2-4k1 2k1+1 + 4k1+2 2k1-1

=

2k1-1

4

；
则k₁-2k₂=k₁-2

2k1-1

4

=

1

2

．

点评：本题考查了圆锥曲线的性质应用，主要考查了学生的化简能力，属于难题．