题目内容
已知过点P（6，8）做两条互相垂直的直线PA、PB，分别交x轴正半轴于A，交y轴正半轴于B，若S△AOB=S△APB，求PA与PB所在直线的方程．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：由题意过OP中点作OP的垂线交x轴于A，交y轴于B，则A，B为所求点，然后过P作PR⊥x轴于R，再借助于三角形相似列比例式求得A，B的坐标，最后由直线方程的两点式求得PA与PB所在直线的方程．
解答：
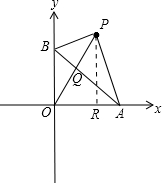解：如图，
由P（6，8），可设OP中点Q（3，4），过Q作QA⊥OP，交x轴于A，交y轴于B，
则PA⊥PB，
过P作PR⊥x轴于R，
|OP|=10，|OQ|=
|OP|=5，
∵Rt△OPR∽Rt△OAQ，（直角、公共角），
∴
=
=
，
∴|OA|=
，|AQ|=
，
∴A（
，0），
又Rt△AOQ∽Rt△ABO，
∴
=
=
，OB=
，
∴B（0，
），
∴PA所在直线方程为：
=
，即24x+7y-200=0；
PB所在直线方程为：
=
，即7x-24y+150=0．
解：如图，由P（6，8），可设OP中点Q（3，4），过Q作QA⊥OP，交x轴于A，交y轴于B，
则PA⊥PB，
过P作PR⊥x轴于R，
|OP|=10，|OQ|=
| 1 |
| 2 |
∵Rt△OPR∽Rt△OAQ，（直角、公共角），
∴
| |OA| |
| |OP| |
| |OQ| |
| |OR| |
| |AQ| |
| |PR| |
∴|OA|=
| 25 |
| 3 |
| 20 |
| 3 |
∴A（
| 25 |
| 3 |
又Rt△AOQ∽Rt△ABO，
∴
| |OB| |
| |OQ| |
| |AQ| |
| |OQ| |
| 4 |
| 3 |
| 25 |
| 4 |
∴B（0，
| 25 |
| 4 |
∴PA所在直线方程为：
| y-0 |
| 8-0 |
x-
| ||
6-
|
PB所在直线方程为：
y-
| ||
8-
|
| x-0 |
| 6-0 |
点评：本题考查了直线方程的求法，解答此题的关键在于由题意正确作出图形，由OP的中点作垂线找到A，B是题眼，是中档题．
练习册系列答案
相关题目
若点O是线段BC外一点，点P是平面上任意一点，且
=λ
+μ
（λ、μ∈R），则下面的说法正确的是（ ）
| OP |
| OB |
| OC |
| A、若λ+μ=1，且λ＞0，则点P在线段BC的延长线上 |
| B、若λ+μ=1，且λ＜0，则点P在线段BC的延长线上 |
| C、若λ+μ＞1，则点P在△OBC外 |
| D、若λ+μ＜1，则点P在△OBC内 |
