题目内容
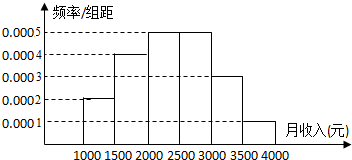
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如右图).为了分析居民的收入与年龄、学历、职业等方面的关系,每隔500元一段要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出的人数为( )

| A、20 | B、25 | C、35 | D、45 |
考点:频率分布直方图
专题:概率与统计
分析:根据频率分布直方图,结合频率、频数与样本容量的关系,即可求出结果.
解答:
解:根据频率分布直方图,得;
在[2500,3000)(元)月收入段的频率是0.0005×500=0.25;
∴在该收入段应抽出的人数为100×0.25=25.
故选:B.
在[2500,3000)(元)月收入段的频率是0.0005×500=0.25;
∴在该收入段应抽出的人数为100×0.25=25.
故选:B.
点评:本题考查了频率分布直方图的应用问题,也考查了频率=
的应用问题,是基础题目.
| 频数 |
| 样本容量 |

练习册系列答案
相关题目
直线bx-ay+c=0(a>0)是曲线y=ln
在x=3处的切线,f(x)=a•2x+b•3x,若f(x+1)>f(x),则x的取值范围是( )
| 1 |
| x |
| A、(-2,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-2,-1) |
已知A(1,2,1),B(-1,3,4),P为AB的中点,则|
|=( )
| AP |
A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
若曲线y=x2+ax+b在点(0,b)处的切线方程是y=x+1,则( )
| A、a=1,b=1 |
| B、a=-1,b=1 |
| C、a=1,b=-1 |
| D、a=-1,b=-1 |