题目内容

若向量
a
=（1，1，x），
b
=（1，2，1），
c
=（1，1，1），满足条件（
c
-
a
）•（2
b
）=-2，则x的值为（　　）
A、1B、2C、3D、4
考点：空间向量的数量积运算
专题：空间向量及应用
分析：根据空间向量的坐标运算，结合题意，求出x的值．
解答： 解：∵向量
a
=（1，1，x），
b
=（1，2，1），
c
=（1，1，1），
且（
c
-
a
）•（2
b
）=-2，
∴（1-1）×2+（1-1）×4+（1-x）×2=-2，
解得x=2，
∴x的值为2．
故选：B．
点评：本题考查了空间向量的坐标运算以及数量积的应用问题，是基础题目．
练习册系列答案
相关题目
若复数z满足方程Z2+2=0，则z=（　　）
A、±
2
i
B、±
2
C、-
2
i
D、-
2
已知函数f（x）=mx2+3（m-2）x-1在区间（-∞，3]上单调减函数，则实数m的取值范围是
 
．
函数y=Asin（ωx+φ）的图象如图：求

（1）A的值；
（2）最小正周期T；
（3）ω的值；
（4）单调递减区间．
设点M是等腰直角三角形ABC的底边AB的中点，P是直线AB上任意一点，PE⊥AC，E为垂足，PF⊥BC，F为垂足．求证：（1）|ME|=|MF|；  
（2）ME⊥MF．
一组数据的茎叶图如图，且平均数为90，则a=（　　）
A、1B、2C、3D、4
一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如右图）．为了分析居民的收入与年龄、学历、职业等方面的关系，每隔500元一段要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500，3000）（元）月收入段应抽出的人数为（　　）
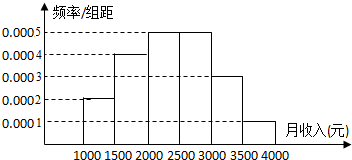
A、20B、25C、35D、45
函数y=sin
πx
2(1+x2)
的值域是（　　）
A、[-1，1]
B、[-
2
2
，
2
2
]
C、[0，1]
D、[-
1
2
，
1
2
]
已知函数f（x）=ax-2
4-ax
-1（a＞0且a≠1）．
（1）求函数f（x）的定义域、值域；
（2）求实数a的取值范围，使得函数f（x）满足：当定义域为[1，+∞）时，f（x）≥0恒成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网