题目内容

佛山某中学高三（1）班排球队和篮球队各有10名同学，现测得排球队10人的身高（单位：cm）分别是：162、170、171、182、163、158、179、168、183、168，篮球队10人的身高（单位：cm）分别是：170、159、162、173、181、165、176、168、178、179．
（Ⅰ） 请把两队身高数据记录在如图4所示的茎叶图中，并指出哪个队的身高数据方差较小（无需计算）；
（Ⅱ） 利用简单随机抽样的方法，分别在两支球队身高超过170cm的队员中各抽取一人做代表，设抽取的两人中身高超过178cm的人数为X，求X的分布列和数学期望．
考点：离散型随机变量的期望与方差,茎叶图,离散型随机变量及其分布列
专题：概率与统计
分析：（Ⅰ） 直接列出茎叶图，判断身高数据方差较小的即可；
（Ⅱ） 利用简单随机抽样的方法，超过170cm的有4人，超过178cm的有3人，篮球队中超过170cm的有5人，超过178cm的有2人，求出X的分布列和然后求解数学期望．
解答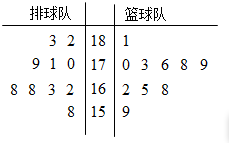： 解：（Ⅰ）茎叶图如图所示，篮球队的身高数据方差较小．…（4分）
（注：写对茎叶图（2分），方差结论正确2分）
（Ⅱ）排球队中超过170cm的有4人，超过178cm的有3人，
篮球队中超过170cm的有5人，超过178cm的有2人，
（注：正确描述人数各（2分），共计4分）
所以X的所有可能取值为0，1，2则…（5分）
（注：正确写出X的值1分）P(X=0)=
C
1
1
C
1
3
C
1
4
C
1
5
=
3
20
，
P（X=1）=
C
1
1
C
1
2
+
C
1
3
C
1
3
C
1
4
C
1
5
=
11
20
，
P（X=2）=
C
1
3
C
1
2
C
1
4
C
1
5
=
6
20
，…（10分）
所以X的分布列为
X012
P
3
20
11
20
6
20
…（11分）
所以X的数学期望EX=0×
3
20
+1×
11
20
+2×
6
20
=
23
20
．…（12分）
点评：本题考查离散型随机变量的分布列以及期望的求法，茎叶图的求法，基本知识的考查．
练习册系列答案
相关题目
圆心为（1，-1），半径为2的圆的方程为（　　）
A、（x+1）2+（y-1）2=4
B、（x-1）2+（y+1）2=2
C、（x-1）2+（y+1）2=4
D、（x+1）2+（y-1）2=2
设a，b，c是实数，3a，4b，5c成等比数列，且
1
a
，
1
b
，
1
c
成等差数列，求
a
c
+
c
a
的值．
双曲线16y2-m2x2=1（m＞0）的一个顶点到它的一条渐近线的距离是
1
5
，则m的值是（　　）
A、1B、2C、3D、4
已知圆M：（x-3）2+（y-4）2=2，四边形ABCD为圆M的内接正方形，E、F分别为边AB、AD的中点，当正方形ABCD绕圆心M转动时，
ME
•
OF
的取值范围是（　　）
A、[-5
2
，5
2
]
B、[-5，5]
C、[-10
2
，10
2
]
D、[-10，10]
某品牌饮料为了扩大其消费市场，特实行“再来一瓶”有奖促销活动．该品牌饮料的瓶盖内或刻有“再来一瓶”字样，或刻有“谢谢惠顾”字样，如见瓶盖内刻有“再来一瓶”字样，即可凭该瓶盖，在指定零售地点兑换相同规格的饮料一瓶，本次活动中奖的概率为
1
5
．今年春节期间有甲、乙、丙3位朋友聚会，选用6瓶这种饮料，并限定每人喝2瓶，求：
（1）甲喝的2瓶饮料都中奖的概率；
（2）甲、乙、丙3人中恰有2人喝到中奖饮料的概率；
（3）记ξ为甲、乙、丙3人中喝到中奖饮料的人数，求ξ的数学期望．
已知
a
，
b
是单位向量，
a
•
b
=0．若向量
c
满足|
c
-
a
-
b
|=2，则|
c
|的取值范围是
 
．
设f（x）是定义在R上的周期为2的函数，当x∈[-1，1]时，f（x）=
1-x2，-1≤x＜0
1
2
x-
1
2
，0≤x＜1
，g（x）是偶函数，当x≥0时，g（x）=
1
2
x，则满足f（x）＞g（x）的实数x的取值范围是
 
．
已知直线x+y+a=0与圆x2+y2=1交于不同的两点A、B，O是坐标原点，且|
OA
+
OB
|≥|
AB
|，那么实数a的取值范围是（　　）
A、(-
2
，-1]∪[1，
2
)
B、(-
2
，0)∪(0，
2
)
C、(-
2
，-1]∪(0，
2
)
D、(-
2
，
2
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网