题目内容
设点（a，b）是区域
内的随机点，函数f（x）=ax2-4bx+1在区间[1，+∞）是增函数的概率为 ．
|
考点：几何概型
专题：概率与统计
分析：作出不等式组对应的平面区域，根据概率的几何概型的概率公式进行计算即可得到结论．
解答：
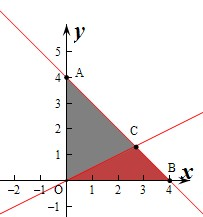解：作出不等式组
内对应的平面区域如图：对应的图形为△OAB，其中对应面积为S=
×4×4=8，
若f（x）=ax2-4bx+1在区间[1，+∞）上是增函数，
则满足a＞0且对称轴x=-
≤1，
即
，对应的平面区域为△OBC，
由
，
解得
，
∴对应的面积为S1=
×
×
=
，
∴根据几何概型的概率公式可知所求的概率为
=
，
故答案为：
．
解：作出不等式组
|
| 1 |
| 2 |
若f（x）=ax2-4bx+1在区间[1，+∞）上是增函数，
则满足a＞0且对称轴x=-
| -4b |
| 2a |
即
|
由
|
解得
|
∴对应的面积为S1=
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
| 16 |
| 9 |
∴根据几何概型的概率公式可知所求的概率为
| ||
| 8 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题主要考查几何概型的概率公式的计算，作出不等式组对应的平面区域是解决本题的关键．
练习册系列答案
相关题目
某车间共有6名工人，他们某日加工零件葛素的茎叶图如图所示，其中茎为十位数，叶为个位数日加工零件大于样本均值的工人为优秀工人，从该车间6名工人中，任取2人，则恰由1名优秀工人的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知为f（x）奇函数，在[3，6]上是增函数，[3，6]上的最大值为8，最小值为-1，则2f（-6）+f（-3）等于（ ）
| A、-15 | B、-13 | C、-5 | D、5 |
函数f（x）=x2+（2a2-6a）x+2在区间（-∞，2]上单调递减，那么实数a的取值范围（ ）
| A、[1，+∞） |
| B、（-∞，2] |
| C、[1，2] |
| D、（-∞，1]∪[2，+∞） |
若函数y=0.5|1-x|+m+1有零点，则m的取值范围是（ ）
| A、m≤-1 |
| B、m≥-2 |
| C、-2＜m≤-1 |
| D、-2≤m＜-1 |