题目内容
13.使f(x)=sin(2x+θ)-$\sqrt{3}$cos(2x+θ)为奇函数,且在[0,$\frac{π}{4}$]上是减函数的θ的一个值是( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
分析 利用辅助角公式化简函数的解析式为2sin(2x+θ-$\frac{π}{3}$),再根据它是奇函数,可得θ=kπ+$\frac{π}{3}$,k∈z.再根据它在[0,$\frac{π}{4}$]上是减函数,分类讨论求得θ的值.
解答 解:∵f(x)=sin(2x+θ)-$\sqrt{3}$cos(2x+θ)=2sin(2x+θ-$\frac{π}{3}$)为奇函数,
∴θ-$\frac{π}{3}$=kπ,∴θ=kπ+$\frac{π}{3}$,k∈Z.
当k为奇数时,令k=2n-1,θ=2nπ-$\frac{2π}{3}$,n∈z,此时f(x)=-2sin2x,满足在[0,$\frac{π}{4}$]上是减函数,
当k为偶数时,令k=2n,θ=2nπ+$\frac{π}{3}$,n∈z,此时f(x)=2sin2x,不满足在[0,$\frac{π}{4}$]上是减函数.
故选:B.
点评 本题主要考查辅助角公式,正弦函数的奇偶性和单调性,体现了分类讨论的数学思想,化简函数的解析式是解题的突破口,属于中档题.

练习册系列答案
相关题目
8.已知椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点分别为F1,F2,M为C上位于第一象限的点,|MF1|=2,且MF1⊥y轴,MF2与椭圆C交于另一点N,若$\overrightarrow{M{F}_{2}}$=2$\overrightarrow{{F}_{2}N}$,则直线MN的斜率为( )
| A. | -$\frac{\sqrt{5}}{2}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
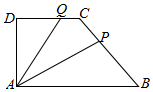 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].