题目内容
4.已知a,b,c分别是△ABC中角A,B,C的对边长,若$A=\frac{π}{3},b=2acosB,c=1$,则S△ABC=$\frac{{\sqrt{3}}}{4}$.分析 利用正弦定理把已知等式化边为角,求出B,可得三角形为等边三角形,则面积可求.
解答 解:△ABC中,∵b=2acosB,
∴根据正弦定理,得sinB=2sinAcosB,
又∵A=$\frac{π}{3}$,
∴sinB=2sin$\frac{π}{3}$cosB,
即sinB=$\sqrt{3}$cosB,可得tanB=$\sqrt{3}$.
∵B∈(0,π),∴B=$\frac{π}{3}$;
∵A=$\frac{π}{3}$,B=$\frac{π}{3}$,
∴C=π-(A+B)=$\frac{π}{3}$.
则a=b=c=1,
∴S△ABC=$\frac{1}{2}×1×1×sin\frac{π}{3}=\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题已知三角形的边和角的关系式,求三角形的面积,着重考查了正弦定理、同角三角函数的基本关系与三角形的面积求法等知识,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
12.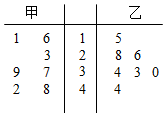 甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
 甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示,$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )| A. | $\overline x$甲>$\overline x$乙,甲比乙得分稳定 | B. | $\overline x$甲>$\overline x$乙,乙比甲得分稳定 | ||
| C. | $\overline x$甲<$\overline x$乙,甲比乙得分稳定 | D. | $\overline x$甲<$\overline x$乙,乙比甲得分稳定 |
16.已知△ABC的内角A、B、C所对的边的长分别是a、b、c.若a2+ab+b2-c2=0,则角C的大小是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
13.使f(x)=sin(2x+θ)-$\sqrt{3}$cos(2x+θ)为奇函数,且在[0,$\frac{π}{4}$]上是减函数的θ的一个值是( )
| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |