题目内容
3．经过A（-3，1），且平行于y轴的直线方程为x=-3．分析 经过点M（-3，1）且平行于y轴的直线上所有点的横坐标为-3，于是得到此直线方程．
解答 解：经过A（-3，1），且平行于y轴的直线方程为：x=-3．
故答案为：x=-3．
点评 本题考查了坐标与图形性质：利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系．
练习册系列答案
相关题目
13．下列函数中满足$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）+f（{x_2}）}}{2}（{x_1}≠{x_2}）$的是（ ）
| A． | f（x）=3x+2 | B． | $f（x）=\sqrt{x}$ | C． | $f（x）=-{（\frac{1}{2}）^x}$ | D． | f（x）=x2+x+1 |
18．下列函数中，既是偶函数又存在零点的是（ ）
| A． | y=x2+1 | B． | y=2|x| | C． | y=lnx | D． | y=cosx |
12．
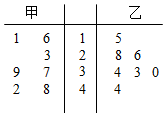甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示，$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分，则下列判断正确的是（ ）
甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示，$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分，则下列判断正确的是（ ）| A． | $\overline x$甲＞$\overline x$乙，甲比乙得分稳定 | B． | $\overline x$甲＞$\overline x$乙，乙比甲得分稳定 | ||
| C． | $\overline x$甲＜$\overline x$乙，甲比乙得分稳定 | D． | $\overline x$甲＜$\overline x$乙，乙比甲得分稳定 |
13．使f（x）=sin（2x+θ）-$\sqrt{3}$cos（2x+θ）为奇函数，且在[0，$\frac{π}{4}$]上是减函数的θ的一个值是（ ）
| A． | $\frac{4π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{3}$ | D． | -$\frac{π}{3}$ |