题目内容
2．已知变量x，y，满足：$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$，则z=2x+y的最大值为4．分析 作出可行域，根据可行域移动目标函数，根据直线的截距得出最优解．
解答 解：作出约束条件表示的可行域如图：
由z=2x+y得y=-2x+z．
由图形可知当直线y=-2x+z经过B点时，直线的截距最大，即z最大．
解方程组$\left\{\begin{array}{l}{2x-y=0}\\{x-2y+3=0}\end{array}\right.$，得B（1，2）．
∴z的最大值为z=2×1+2=4．
故答案为：4．
点评 本题考查了简单的线性规划，属于中档题．
练习册系列答案
相关题目
12．
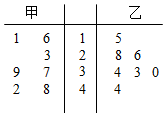甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示，$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分，则下列判断正确的是（ ）
甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示，$\overline x$甲、$\overline x$乙分别表示甲、乙两人的平均得分，则下列判断正确的是（ ）| A． | $\overline x$甲＞$\overline x$乙，甲比乙得分稳定 | B． | $\overline x$甲＞$\overline x$乙，乙比甲得分稳定 | ||
| C． | $\overline x$甲＜$\overline x$乙，甲比乙得分稳定 | D． | $\overline x$甲＜$\overline x$乙，乙比甲得分稳定 |
13．使f（x）=sin（2x+θ）-$\sqrt{3}$cos（2x+θ）为奇函数，且在[0，$\frac{π}{4}$]上是减函数的θ的一个值是（ ）
| A． | $\frac{4π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{3}$ | D． | -$\frac{π}{3}$ |
7．已知向量法$\overrightarrow{{l}_{1}}$≠$\overrightarrow{0}$，λ∈R，$\overrightarrow{a}$=$\overrightarrow{{l}_{1}}$+λ$\overrightarrow{{l}_{2}}$，$\overrightarrow{b}$=2$\overrightarrow{{l}_{2}}$，若向量$\overrightarrow{a}$和$\overrightarrow{b}$共线，则下列关系一定成立的是（ ）
| A． | λ=0 | B． | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$ | C． | $\overrightarrow{{l}_{1}}$∥$\overrightarrow{{l}_{2}}$ | D． | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$或λ=0 |
11．A，B，C是△ABC的三个内角，若$\overrightarrow{m}$=（sin2$\frac{B+C}{2}$，1），$\overrightarrow{n}$=（-2，cos2A+1），且$\overrightarrow{m}$⊥$\overrightarrow{n}$，则cosA=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$或1 | D． | $\frac{1}{2}$或0 |
6．小明、小王、小张、小李4名同学排成一纵队表演节目，其中小明不站排头，小张不站排尾，则不同的排法共有（ ）种．
| A． | 14 | B． | 18 | C． | 12 | D． | 16 |