题目内容
已知函数f(x)=
,若对于正数kn(n∈N*),直线y=knx与函数y=f(x)的图象恰有2n+1个不同交点,则数列{kn2}的前n项和为 .
|
考点:数列的求和
专题:综合题,函数的性质及应用,等差数列与等比数列
分析:可知y=f(x)的图象是一系列半径为1的半圆,由题意知直线y=knx与第n+1个半圆相切,由此可求kn2,然后利用裂项相消法可求答案.
解答:
解:函数y=f(x)的图象是一系列半径为1的半圆,
∵直线y=knx与函数y=f(x)的图象恰有2n+1个不同交点,
∴直线y=knx与第n+1个半圆相切,∴
=1,
=
=
(
-
),
∴
+
+…+
=
.
故答案为:
.
∵直线y=knx与函数y=f(x)的图象恰有2n+1个不同交点,
∴直线y=knx与第n+1个半圆相切,∴
| (2n+1)kn | ||||
|
| k | 2 n |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| k | 2 1 |
| k | 2 2 |
| k | 2 n |
| n |
| 4n+4 |
故答案为:
| n |
| 4n+4 |
点评:该题考查数列的求和、直线与圆的位置关系,裂项相消法对数列求和是高考考查的重点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
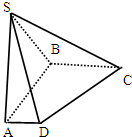 如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )
如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
数列{an}中,已知a1=5,an=an-1+3(n≥2),则数列{an}的第三项为( )
| A、5 | B、8 | C、11 | D、14 |
已知
-
=-8
+16
,
+
=2
-8
(
,
为互相垂直的单位向量),则
•
=( )
| a |
| b |
| i |
| j |
| a |
| b |
| i |
| j |
| i |
| j |
| a |
| b |
| A、63 | B、-63 |
| C、33 | D、-33 |
 如图,F1,F2分别是椭圆C:
如图,F1,F2分别是椭圆C: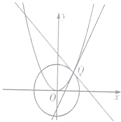 如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=
如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=