题目内容
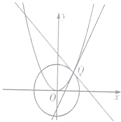 如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=
如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=考点:圆与圆锥曲线的综合
专题:计算题,圆锥曲线的定义、性质与方程
分析:设Q(m,n),则圆O在Q处的切线方程为mx+ny=1,则k1=-
,求导数可得k2=
,利用k1+k2=1,可得-
+
=1,
结合m2=2pn,m2+n2=1,即可求出p的值.
| m |
| n |
| m |
| p |
| m |
| n |
| m |
| p |
结合m2=2pn,m2+n2=1,即可求出p的值.
解答:
解:设Q(m,n),则圆O在Q处的切线方程为mx+ny=1,则k1=-
,
∵抛物线C:x2=2py,∴y′=
,∴k2=
,
∵k1+k2=1,
∴-
+
=1,
∵m2=2pn,m2+n2=1,
∴p=
,m=n=
,
故答案为:
.
| m |
| n |
∵抛物线C:x2=2py,∴y′=
| x |
| p |
| m |
| p |
∵k1+k2=1,
∴-
| m |
| n |
| m |
| p |
∵m2=2pn,m2+n2=1,
∴p=
| ||
| 4 |
| ||
| 2 |
故答案为:
| ||
| 4 |
点评:本题考查圆与圆锥曲线的综合,考查切线斜率的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
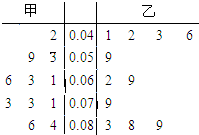 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )| A、甲 | B、乙 |
| C、甲乙相等 | D、无法确定 |
向量
=(1,-2),
=(2,1),则( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
长方体的表面积是24,所有棱长的和是24,则对角线的长是( )
A、
| ||
| B、4 | ||
C、3
| ||
D、2
|
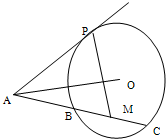 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为