题目内容
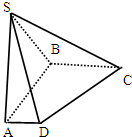 如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )
如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:设点B到平面SCD的距离为h,利用VS-BCD=VB-SCD,即可求得结论.
解答:
解:∵底面ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=BC=2
∴S△BCD=2,
∵侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,
∴SD=CD=
,SC=2
,
∴S△SCD=
•2
•
=
,
设点B到平面SCD的距离为h,则
∵VS-BCD=VB-SCD,
∴
•2•2=
•
h,
∴h=
.
∴点B到平面SCD的距离为
.
故答案为:
.
∴S△BCD=2,
∵侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,
∴SD=CD=
| 5 |
| 3 |
∴S△SCD=
| 1 |
| 2 |
| 3 |
| 5-3 |
| 6 |
设点B到平面SCD的距离为h,则
∵VS-BCD=VB-SCD,
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
∴h=
2
| ||
| 3 |
∴点B到平面SCD的距离为
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查点、线、面间的距离计算,考查体积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
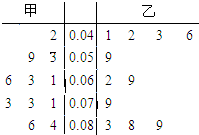 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )| A、甲 | B、乙 |
| C、甲乙相等 | D、无法确定 |
用数学归纳法证明
+
+…+
≥
,从n=k到n=k+l,不等式左边需添加的项是( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 5 |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
向量
=(1,-2),
=(2,1),则( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆C:
+
=1(a>0,b>0)的右焦点为F,椭圆C与过原点的直线相交于A、B两点,连接AF、BF,若|AB|=8,|BF|=4,且cos∠ABF=
,则椭圆C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m、n、l为直线,α、β、γ为平面,下列命题为真命题的是( )
| A、若m∥α,m∥β,则α∥β |
| B、若m?α,n?β,α⊥β,则m⊥n |
| C、若l⊥n,l⊥m,m?α,n?α,则l⊥α |
| D、若α⊥β,α∥γ,则β⊥γ |
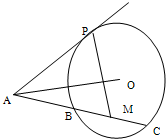 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为