题目内容
设数列{an}的前n项和为Sn,满足Sn=2an-2n(n∈N*),令bn=
.
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的前n项和Sn.
| an |
| 2n |
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:综合题,等差数列与等比数列
分析:(1)由Sn=2an-2n(n∈N*),可得n≥2时,Sn-1=2an-1-2n-1(n∈N*),两式相减,结合bn=
,即可证明数列{bn}为等差数列;
(2)确定an=(n+1)•2n-1,再利用错位相减法,可求数列{an}的前n项和Sn.
| an |
| 2n |
(2)确定an=(n+1)•2n-1,再利用错位相减法,可求数列{an}的前n项和Sn.
解答:
(1)证明:因为Sn=2an-2n(n∈N*),所以n≥2时,Sn-1=2an-1-2n-1(n∈N*),
所以an=2an-2n-(2an-1-2n-1),
即an=2an-1-2n-1.
由a1=2a1-2得a1=2.
由bn=
得b1=1.
当n≥2时,bn-bn-1=
,
所以{bn}是首项为1,公差为
的等差数列.
(2)解:由(1)知,bn=
,即
=
,
所以{an}的通项公式为an=(n+1)•2n-1.
所以Sn=2•20+3•21+…+(n+1)•2n-1,①
∴2Sn=2•21+3•22+…+(n+1)•2n,②
由①-②得-Sn=2•20+21+22+…+2n-1-(n+1)•2n,
∴Sn=n•2n.
所以an=2an-2n-(2an-1-2n-1),
即an=2an-1-2n-1.
由a1=2a1-2得a1=2.
由bn=
| an |
| 2n |
当n≥2时,bn-bn-1=
| 1 |
| 2 |
所以{bn}是首项为1,公差为
| 1 |
| 2 |
(2)解:由(1)知,bn=
| n+1 |
| 2 |
| an |
| 2n |
| n+1 |
| 2 |
所以{an}的通项公式为an=(n+1)•2n-1.
所以Sn=2•20+3•21+…+(n+1)•2n-1,①
∴2Sn=2•21+3•22+…+(n+1)•2n,②
由①-②得-Sn=2•20+21+22+…+2n-1-(n+1)•2n,
∴Sn=n•2n.
点评:本题考查等差数列的证明,考查数列的通项与求和,确定数列的通项是关键.

练习册系列答案
相关题目
在棱长为2的正方体ABCD-A1B1C1D1中,M、N分别是A1B1、BB1的中点,那么直线AM与CN所成的角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC的内角A、B、C所对的边分别为a,b,c.若B=2A,a=1,b=
,则这样的三角形有( )
| 2 |
| A、只有一个 | B、有两个 |
| C、不存在 | D、无数个 |
复数i3的值是( )
| A、-i | B、1 | C、-1 | D、i |
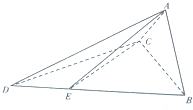 如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=