题目内容
在棱长为2的正方体ABCD-A1B1C1D1中,M、N分别是A1B1、BB1的中点,那么直线AM与CN所成的角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:建立空间直角坐标系D-xyz,利用向量法能求出直线AM与CN所成的角的余弦值.
解答:
 解:如图,建立空间直角坐标系D-xyz,
解:如图,建立空间直角坐标系D-xyz,
由题意知A(2,0,0),M(2,1,2),
C(0,2,0),N(2,2,1),
∴
=(0,1,2),
=(2,0,1),
设直线AM与CN所成的角为θ,
则cosθ=|cos<
,
>|=|
|=
.
∴直线AM与CN所成的角的余弦值是
.
故选:D.
 解:如图,建立空间直角坐标系D-xyz,
解:如图,建立空间直角坐标系D-xyz,由题意知A(2,0,0),M(2,1,2),
C(0,2,0),N(2,2,1),
∴
| AM |
| CN |
设直线AM与CN所成的角为θ,
则cosθ=|cos<
| AM |
| CN |
| 2 | ||||
|
| 2 |
| 5 |
∴直线AM与CN所成的角的余弦值是
| 2 |
| 5 |
故选:D.
点评:本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
数列{an}满足a0=
,an+1=[an]+
,([an]与{an}分别表示an的整数部分与分数部分),则a2014=( )
| 3 |
| 1 |
| {an} |
A、3020+
| ||||
B、3020+
| ||||
C、
| ||||
D、3018+
|
用10元、5元和1元来支付20元钱的书款,不同的支付方法有( )
| A、3 | B、5 | C、9 | D、12 |
对下面三件事:
①科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈;
②某班数学成绩有15人在120分以上,40人在90~119分之间,1人不及格,现从中抽出8人研讨,进一步改进教与学;
③某中学的15名艺术特长生中选出3人调查学习负担情况.
所采用的抽样方法依次为( )
①科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈;
②某班数学成绩有15人在120分以上,40人在90~119分之间,1人不及格,现从中抽出8人研讨,进一步改进教与学;
③某中学的15名艺术特长生中选出3人调查学习负担情况.
所采用的抽样方法依次为( )
| A、简单随机抽样,分层抽样,简单随机抽样 |
| B、系统抽样,系统抽样,简单随机抽样 |
| C、分层抽样,简单随机抽样,简单随机抽样 |
| D、系统抽样,分层抽样,简单随机抽样 |
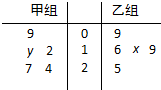 如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )
如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )| A、7,8 | B、5,7 |
| C、8,5 | D、8,7 |
函数f(x)=xlnx在x=1处的切线为( )
| A、y=x+1 |
| B、y=x-1 |
| C、y=1-x |
| D、y=1-2x |
O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=3.则△POF的面积为( )
A、
| ||
B、2
| ||
C、
| ||
D、2
|