题目内容
已知函数f(x)=x+
,若关于x的方程f2(x)-(m+1)f(x)+2m=0有四个不同的实数根,则实数m的取值范围是多少?
| 1 |
| x |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:令t=f(x)=x+
,则 t≥2,或t≤-2,关于t的一元二次方程t2-(m+1)t+2m=0有两个实数根,且这2个实数根大于2或小于-2.令f(t)=t2-(m+1)t+2m,再分①若这两个根都大于2,②若这两个根都小于-2,若这两个根一个大于2,另一个小于-2,三种情况,分别求得m的范围,再取并集,即得所求.
| 1 |
| x |
解答:
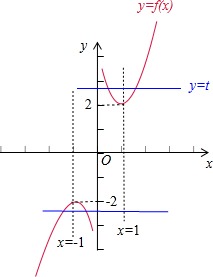 解:∵关于x的方程f2(x)-(m+1)f(x)+2m=0
解:∵关于x的方程f2(x)-(m+1)f(x)+2m=0
有4个不同的实数根,
令t=f(x)=x+
,则 t≥2,或t≤-2,
故关于t的一元二次方程t2-(m+1)t+2m=0有两个实数根,且这2个实数根大于2或小于-2.
令f(t)=t2-(m+1)t+2m,
①若这两个根都大于2,
则由
,求得 m>2+
.
②若这两个根都小于-2,
则由
,求得 m∈∅.
③若这两个根一个大于2,另一个小于-2,则由
,可得m∈∅.
综上可得,m的范围为(2+
,+∞).
 解:∵关于x的方程f2(x)-(m+1)f(x)+2m=0
解:∵关于x的方程f2(x)-(m+1)f(x)+2m=0有4个不同的实数根,
令t=f(x)=x+
| 1 |
| x |
故关于t的一元二次方程t2-(m+1)t+2m=0有两个实数根,且这2个实数根大于2或小于-2.
令f(t)=t2-(m+1)t+2m,
①若这两个根都大于2,
则由
|
| 3 |
②若这两个根都小于-2,
则由
|
③若这两个根一个大于2,另一个小于-2,则由
|
综上可得,m的范围为(2+
| 3 |
点评:本题主要考查方程根的个数判断,体现了转化、分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
O为坐标原点,F为抛物线C:y2=4x的焦点,P为C上一点,若|PF|=3.则△POF的面积为( )
A、
| ||
B、2
| ||
C、
| ||
D、2
|
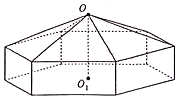 一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.
一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.