题目内容
已知p：函数y=log2（x2+2x-3）有意义，q：1＜2x＜4，r：（x-m+1）（x-m-1）＜0
（Ⅰ）若p且q是真命题，求x的取值范围；
（Ⅱ）若p是r的必要条件，求m的取值范围．
（Ⅰ）若p且q是真命题，求x的取值范围；
（Ⅱ）若p是r的必要条件，求m的取值范围．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：（Ⅰ）根据复合命题之间的关系，即可得到若p且q是真命题，则p，q为真命题，即可求x的取值范围；
（Ⅱ）根据p是r的必要条件，建立条件关系，即可求m的取值范围．
（Ⅱ）根据p是r的必要条件，建立条件关系，即可求m的取值范围．
解答：
解：（I）若p为真，则x2+2x-3＞0，解得x＜-3或x＞1
若q为真，则1＜2x＜4，解得0＜x＜2，
若“p且q”是真命题，
则
，
解得1＜x＜2．
（II）若r为真，则（x-m+1）（x-m-1）＜0，
即 m-1＜x＜m+1，
因为p是r的必要条件
所有{x|m-1＜x＜m+1}⊆{x|x＜-3或x＞1}，
即m+1≤-3或m-1≥1，
解得m≤-4或m≥2．
若q为真，则1＜2x＜4，解得0＜x＜2，
若“p且q”是真命题，
则
|
解得1＜x＜2．
（II）若r为真，则（x-m+1）（x-m-1）＜0，
即 m-1＜x＜m+1，
因为p是r的必要条件
所有{x|m-1＜x＜m+1}⊆{x|x＜-3或x＞1}，
即m+1≤-3或m-1≥1，
解得m≤-4或m≥2．
点评：本题主要考查复合函数的真假关系，以及充分条件和必要条件的应用，利用不等式的解法求出命题的等价条件是解决本题的关键．
练习册系列答案
相关题目
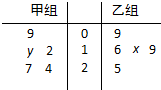如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩（单位：分），已知甲组数据的中位数为17，乙组数据的平均数为17.4，则x，y的值分别为（ ）| A、7，8 | B、5，7 |
| C、8，5 | D、8，7 |
在等差数列{an}中，a1+a2+a3=3，a28+a29+a30=165，则此数列前30项和等于（ ）
| A、810 | B、840 |
| C、870 | D、900 |