题目内容
已知F(1,0)椭圆C1的右焦点且F为双曲线C2的右顶点,椭圆C1与双曲线C2的一个交点是M(
,
).
(Ⅰ)求椭圆C1及双曲线C2的方程;
(Ⅱ)若点P是双曲线右支上的动点,直线PF交y轴于点Q,试问以线段PQ为直径的圆是否恒过定点?证明你的结论.
2
| ||
| 3 |
| ||
| 3 |
(Ⅰ)求椭圆C1及双曲线C2的方程;
(Ⅱ)若点P是双曲线右支上的动点,直线PF交y轴于点Q,试问以线段PQ为直径的圆是否恒过定点?证明你的结论.
考点:圆与圆锥曲线的综合,椭圆的标准方程,双曲线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用待定系数法,结合椭圆的定义,即可求椭圆C1及双曲线C2的方程;
(Ⅱ)直线PF2的方程为y=
(x-1),得Q(0,-
),证明
•
=0,即可得出结论.
(Ⅱ)直线PF2的方程为y=
| y0 |
| x0-1 |
| y0 |
| x0-1 |
| F1P |
| F1Q |
解答:
解:(Ⅰ)由题意设椭圆C1的方程是
+
=1,双曲线C2的方程是x2-
=1,…1分
则2a1=|MF1|+|MF2|=
+
=2
,
∴a1=
,b1=1,椭圆C1的方程是
+y2=1,…4分
由点M在双曲线上得:
-
=1,得b22=1,
∴双曲线C2的方程是x2-y2=1,…6分
(Ⅱ)设P(x0,y0),则x02-y02=1,
直线PF2的方程为y=
(x-1),得Q(0,-
),
∴
=(x0+1,y0),
=(1,-
),
∴
•
=(x0+1)-y0•
=0,
∴
⊥
,
∴以线段PQ为直径的圆恒过定点F1(-1,0).,…12分
| x2 |
| a12 |
| y2 |
| b12 |
| y2 |
| b22 |
则2a1=|MF1|+|MF2|=
|
|
| 2 |
∴a1=
| 2 |
| x2 |
| 2 |
由点M在双曲线上得:
| 4 |
| 3 |
| 1 |
| 3b22 |
∴双曲线C2的方程是x2-y2=1,…6分
(Ⅱ)设P(x0,y0),则x02-y02=1,
直线PF2的方程为y=
| y0 |
| x0-1 |
| y0 |
| x0-1 |
∴
| F1P |
| F1Q |
| y0 |
| x0-1 |
∴
| F1P |
| F1Q |
| y0 |
| x0-1 |
∴
| F1P |
| F1Q |
∴以线段PQ为直径的圆恒过定点F1(-1,0).,…12分
点评:本题考查椭圆、双曲线的标准方程,考查直线与双曲线的位置关系,考查恒过定点问题,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列{an}的前n项和为Sn,若a1=1,a2+a3=11,则S6-S3=( )
| A、27 | B、39 | C、45 | D、63 |
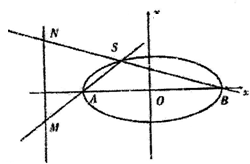 如图,已知椭圆C:
如图,已知椭圆C: 设椭圆
设椭圆