题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为e=
,椭圆上的点P与两个焦点F1,F2构成的三角形的最大面积为1,
(1)求椭圆C的方程;
(2)若点Q为直线x+y-2=0上的任意一点,过点Q作椭圆C的两条切线QD、QE(切点分别为D、E),试证明动直线DE恒过一定点,并求出该定点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)若点Q为直线x+y-2=0上的任意一点,过点Q作椭圆C的两条切线QD、QE(切点分别为D、E),试证明动直线DE恒过一定点,并求出该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆C的方程.
(2)设切点为D(x1,y1),E(x2,y2),则切线方程为x1x+2y1y=2,x2x+2y2y=2,由已知条件推导出D(x1,y1),E(x2,y2),都在直线mx+2(2-m)y=2上,由此能证明动直线DE恒过一定点(1,
).
|
(2)设切点为D(x1,y1),E(x2,y2),则切线方程为x1x+2y1y=2,x2x+2y2y=2,由已知条件推导出D(x1,y1),E(x2,y2),都在直线mx+2(2-m)y=2上,由此能证明动直线DE恒过一定点(1,
| 1 |
| 2 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率为e=
,
椭圆上的点P与两个焦点F1,F2构成的三角形的最大面积为1,
∴
,解得a=
,b=c=1,
∴椭圆C的方程为
+y2=1.
(2)证明:设切点为D(x1,y1),E(x2,y2),
则切线方程为x1x+2y1y=2,x2x+2y2y=2,
∵两条切线都过x+y-2=0上任意一点Q(m,2-m),
∴得到x1m+2y1(2-m)=2,x2m+2y2(2-m)=2,
∴D(x1,y1),E(x2,y2),都在直线mx+2(2-m)y=2上,
而对任意的m,直线mx+2(2-m)y=2始终经过定点(1,
).
∴动直线DE恒过一定点(1,
).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
椭圆上的点P与两个焦点F1,F2构成的三角形的最大面积为1,
∴
|
| 2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)证明:设切点为D(x1,y1),E(x2,y2),
则切线方程为x1x+2y1y=2,x2x+2y2y=2,
∵两条切线都过x+y-2=0上任意一点Q(m,2-m),
∴得到x1m+2y1(2-m)=2,x2m+2y2(2-m)=2,
∴D(x1,y1),E(x2,y2),都在直线mx+2(2-m)y=2上,
而对任意的m,直线mx+2(2-m)y=2始终经过定点(1,
| 1 |
| 2 |
∴动直线DE恒过一定点(1,
| 1 |
| 2 |
点评:本题考查椭圆方程的求法,考查动直线恒过定点的证明,解题时要认真审题,注意椭圆的切线方程的合理运用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
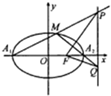 如图,A1(-2,0),A2(2,0)是椭圆C:
如图,A1(-2,0),A2(2,0)是椭圆C: 若椭圆E1:
若椭圆E1: