题目内容
 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4,AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在线段AD上,且PG=4,AG=| 1 |
| 3 |
(1)求异面直线GE与PC所成角的余弦值;
(2)求DG与平面PBG所成角的大小.
考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:(1)以G点为原点建立空间直角坐标系G-xyz,求出
=(1,1,0),
=(0,2,-4),利用向量的夹角公式,即可求异面直线GE与PC所成角的余弦值;
(2)求出平面PBG的一个法向量,利用向量的夹角公式,即可求DG与平面PBG所成角的大小.
| GE |
| PC |
(2)求出平面PBG的一个法向量,利用向量的夹角公式,即可求DG与平面PBG所成角的大小.
解答:
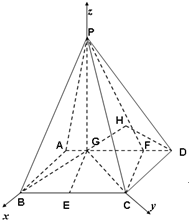 解:(1)如图所示,以G点为原点建立空间直角坐标系G-xyz,则B(2,0,0),C(0,2,0),P(0,0,4)
解:(1)如图所示,以G点为原点建立空间直角坐标系G-xyz,则B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0),∴
=(1,1,0),
=(0,2,-4),
∴cos<
,
>=
=
=
,
∴异面直线GE与PC所成角的余弦值为
;---(6分)
(2)
=
=(-
,
,0),
=(2,0,0),
=(0,0,4),
设平面PBG的一个法向量为
=(x,y,z),则
,可得
=(0,1,0)
设DG与平面PBG所成角为α,则sinα=|cos<
,
>|=
=
,
∴α=45°,即DG与平面PBG所成角为45°.
 解:(1)如图所示,以G点为原点建立空间直角坐标系G-xyz,则B(2,0,0),C(0,2,0),P(0,0,4)
解:(1)如图所示,以G点为原点建立空间直角坐标系G-xyz,则B(2,0,0),C(0,2,0),P(0,0,4)故E(1,1,0),∴
| GE |
| PC |
∴cos<
| GE |
| PC |
| ||||
|
|
| 2 | ||||
|
| ||
| 10 |
∴异面直线GE与PC所成角的余弦值为
| ||
| 10 |
(2)
| GD |
| 3 |
| 4 |
| BC |
| 3 |
| 2 |
| 3 |
| 2 |
| GB |
| GP |
设平面PBG的一个法向量为
| n |
|
| n |
设DG与平面PBG所成角为α,则sinα=|cos<
| GD |
| n |
| ||||
|
| ||
| 2 |
∴α=45°,即DG与平面PBG所成角为45°.
点评:本题考查空间角,考查向量知识的运用,正确运用向量的夹角公式是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目




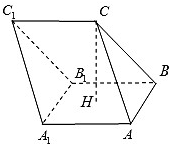 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.