题目内容
设集合M={-1，1}，N={a2}，则“a=1”是“M∪N=M”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据集合关系，利用充分条件和必要条件的定义即可得到结论．
解答：
解：若M∪N=M，则N⊆M，
若a=1，则N={a2}={1}，满足N⊆M，充分性成立，
若M∪N=M，即N⊆M，则a2=1，解得a=±1，必要性不成立，
故“a=1”是“M∪N=M”的充分不必要条件，
故选：A．
若a=1，则N={a2}={1}，满足N⊆M，充分性成立，
若M∪N=M，即N⊆M，则a2=1，解得a=±1，必要性不成立，
故“a=1”是“M∪N=M”的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的判定，利用集合之间的关系是解决本题的关键，比较基础．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
等比数列{an}中，a1＞0，则“a1＜a3”是“a3＜a4”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知A={x|x＞-1}，B={x|2x＜4}，则A∩B=（ ）
| A、{x|x＜2} |
| B、{x|x＞-1} |
| C、{x|-1＜x＜2} |
| D、{x|0＜x＜2} |
各项均为正数的等比数列{an}中，a2a5a8=8，则log2a4+log2a6=（ ）
| A、1 | B、2 | C、3 | D、4 |
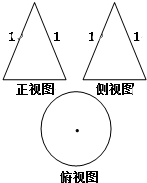如图，一个几何体的正视图和侧视图是腰长为1的等腰三角形，俯视图是一个圆及其圆心，当这个几何体的体积最大时圆的半径是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知对于正项数列{an}满足am+n=am•an（m，n∈N*），若a2=9，则log3a1+log3a2+…+log3a12=（ ）
| A、40 | B、66 | C、78 | D、156 |