题目内容
已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=|x-a2|+|x-3a2|-4a2.若对任意x∈R,f(x)≤f(x+2),则实数a的取值范围为 .
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:由于当x>0时,f(x)=|x-a2|+|x-3a2|-4a2.可得当当0<x≤a2时,f(x)=-2x;当a2<x≤3a2时,f(x)=-2a2;当x>3a2时,f(x)=2x-8a2.画出其图象.由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象.由于x∈R,f(x)≤f(x+2)可得8a2≤2,解出即可.
解答:
解:∵当x>0时,f(x)=|x-a2|+|x-3a2|-4a2.
∴当0<x≤a2时,f(x)=a2-x+3a2-x-4a2=-2x;
当a2<x≤3a2时,f(x)=x-a2+3a2-x-4a2=-2a2;
当x>3a2时,f(x)=x-a2+x-3a2-4a2=2x-8a2.
画出其图象如下:
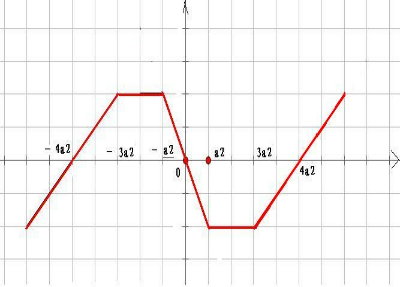
由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,与x>0时的图象关于原点对称.
∵?x∈R,f(x+2)≥f(x),
∴8a2≤2,
解得a∈[-
,
].
∴实数a的取值范围为[-
,
].
故答案为:[-
,
].
∴当0<x≤a2时,f(x)=a2-x+3a2-x-4a2=-2x;
当a2<x≤3a2时,f(x)=x-a2+3a2-x-4a2=-2a2;
当x>3a2时,f(x)=x-a2+x-3a2-4a2=2x-8a2.
画出其图象如下:

由于函数f(x)是定义在R上的奇函数,即可画出x<0时的图象,与x>0时的图象关于原点对称.
∵?x∈R,f(x+2)≥f(x),
∴8a2≤2,
解得a∈[-
| 1 |
| 2 |
| 1 |
| 2 |
∴实数a的取值范围为[-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数奇偶性、周期性,考查了分类讨论的思想方法,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
 如图为一半径为2的扇形(其中扇形中心角为90°),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为( )
如图为一半径为2的扇形(其中扇形中心角为90°),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
D、1-
|