题目内容
若点M是△ABC所在平面内的一点，且满足|3
-
-
|=0，则△ABM与△ABC面积之比等于（ ）
| AM |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：向量的模
专题：平面向量及应用,推理和证明
分析：点M是△ABC所在平面内的一点，且满足|3
-
-
|=0，
根据向量的概念，运算求解；3
-
-
=
，
+
=2
，
3
=2
，
，根据△ABG和△ABC面积的关系，△ABM与△ABC面积之比，求出面积之比．
| AM |
| AB |
| AC |
根据向量的概念，运算求解；3
| AM |
| AB |
| AC |
| 0 |
| AB |
| AC |
| AG |
3
| AM |
| AG |
|
| ||
|
|
解答：
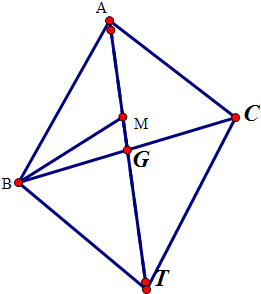解：如图G为BC的中点，
点M是△ABC所在平面内的一点，且满足|3
-
-
|=0，
3
-
-
=
，
+
=2
，
3
=2
，
=
，
∵△ABG和△ABC的底相等，
∴S△ABG=
S△ABC，
=
，
即△ABM与△ABC面积之比：
×
=
，
故选；C
解：如图G为BC的中点，点M是△ABC所在平面内的一点，且满足|3
| AM |
| AB |
| AC |
3
| AM |
| AB |
| AC |
| 0 |
| AB |
| AC |
| AG |
3
| AM |
| AG |
|
| ||
|
|
| 2 |
| 3 |
∵△ABG和△ABC的底相等，
∴S△ABG=
| 1 |
| 2 |
| S△ABM |
| S△ABG |
| 2 |
| 3 |
即△ABM与△ABC面积之比：
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
故选；C
点评：本题考查了向量的几何运算，根据线段的比值，面积的关系求解，注意几何图形中线段的关系．
练习册系列答案
相关题目
如图为一半径为2的扇形（其中扇形中心角为90°），在其内部随机地撒一粒黄豆，则它落在阴影部分的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、1-
|
下列不等式（1）m-3＞m-5；（2）5-m＞3-m；（3）5m＞3m；（4）5+m＞5-m其中正确的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |