题目内容

9．若函数f（x）=x3-3bx+3b在（0，1）内有极小值，则实数b的取值范围是（　　）
A．（0，1）B．（-∞，1）C．（0，+∞）D．$（-∞，\frac{1}{2}）$

分析 首先求出函数的导数，然后令导数为零，求出函数的极值，最后确定b的范围．

解答 解：由题意得f′（x）=3x2-3b，
令f′（x）=0，则x=±$\sqrt{b}$，（负值舍去）
又∵函数f（x）=x3-3bx+3b在区间（0，1）内有极小值，
∴0＜$\sqrt{b}$＜1，解得：0＜b＜1，
∴实数b的取值范围（0，1），
故选：A．

点评 熟练运用函数的导数求解函数的极值问题，同时考查了分析问题的能力，属于基础题．

练习册系列答案
相关题目
19．若曲线C的参数方程为$\left\{\begin{array}{l}x=2cosθ\\ y=1+2sinθ\end{array}\right.$（参数$θ∈[{-\frac{π}{2}，\frac{π}{2}}]$），则曲线C（　　）
A．表示直线B．表示线段C．表示圆D．表示半个圆
20．在直角坐标系中xOy，直线C1的参数方程为$\left\{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}\right.$（t是参数）．在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρ=sinθ-cosθ（θ是参数）．
（Ⅰ）将曲线C2的极坐标方程化为直角坐标方程，并判断曲线C2所表示的曲线；
（Ⅱ）若M为曲线C2上的一个动点，求点M到直线C1的距离的最大值和最小值．
17．已知函数 f（x）=|2x+1-|2x-t|（t∈R）．
　　（Ⅰ）当 t=3时，解关于x 的不等式 f（x）＜1；
　　（Ⅱ）?x∈R使得，求 f（x）≤-5，求t的取值范围．
4．已知向量$\overrightarrow a=（1，0），\overrightarrow b=（0，1），\overrightarrow c=\overrightarrow a+λ\overrightarrow b（λ∈R）$，向量$\overrightarrow d$如图表示，则（　　）
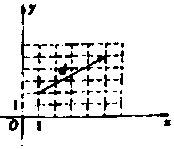
A．?λ＞0，使得$\overrightarrow c⊥\overrightarrow d$B．?λ＞0，使得＜$\overrightarrow{c}$，$\overrightarrow{d}$＞=60°
C．?λ＜0，使得＜$\overrightarrow{c}$，$\overrightarrow{d}$＞=30°D．?λ＞0，使得$\overrightarrow c=m\overrightarrow d（m$为不为0的常数）
14．已知x的不等式|x+3|-|x-1|≤a2-3a，其中a为实数．
（1）当a=1时，解不等式；
（2）若不等式的解集为R，求a的取值范围．
1．已知函数y=f（x）图象关于y轴对称的图象对应的函数为y=F（x），当函数y=f（x）和y=F（x）在区间[a，b]同时递增或同时递减时，区间[a，b]叫做函数y=f（x）的“不动区间”．若区间[1，2]为函数y=|2x-t|的“不动区间”，则实数t的最大值为2．
18．如图是把二进制数11111（2）化为十进制数的一个程序框图，则输出的S=（　　）
 
A．15B．30C．31D．63
19．已知A，B，C三点都在体积为$\frac{500π}{3}$的球O的表面上，若AB=4，∠ACB=30°，则球心O到平面ABC的距离为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网