题目内容
函数y=
的值域是 ．
| lg(-3x2+6x+7) |
考点：函数的值域
专题：函数的性质及应用
分析：求出函数y的表达式中二次根式的被开方数取值范围，即得函数的值域．
解答：
解：∵函数y=
，
∴二次根式的被开方数lg（-3x2+6x+7）≥0，
∴设函数t=-3x2+6x+7，
则当x=-
=1时，t取得最大值10，
∴lg（-3x2+6x+7）的最大值是lg10=1，
∴函数y的值域是[0，1]；
故答案为：[0，1]．
| lg(-3x2+6x+7) |
∴二次根式的被开方数lg（-3x2+6x+7）≥0，
∴设函数t=-3x2+6x+7，
则当x=-
| 6 |
| 2×(-3) |
∴lg（-3x2+6x+7）的最大值是lg10=1，
∴函数y的值域是[0，1]；
故答案为：[0，1]．
点评：本题考查了求函数值域的问题，解题的关键是求出二次根式的被开方数的取值范围，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC=CD，过C作圆O的切线交AD于E．若AB=8，DC=4，则DE=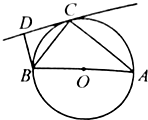
如图，⊙O的直径AB=4，C为圆周上一点，AC=3，CD是⊙O的切线，BD⊥CD于D，则CD=