Question

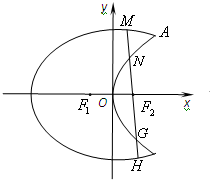我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C”是由椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)与抛物线y²=4x中两段曲线弧合成，F₁、F₂为椭圆的左、右焦点，F₂（1，0），A为椭圆与抛物线的一个公共点，|AF2|=

5

2

．
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在过F₂的一条直线l，与“盾圆C”依次交于M、N、G、H四点，使得△F₁MH与△F₁NG的面积比为6：5？若存在，求出直线l方程；若不存在，说明理由．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）先求出A的坐标，利用焦点坐标，结合椭圆的定义，即可求椭圆的方程；
（Ⅱ）设直线l为x=my+1（m≠0），代入椭圆方程与抛物线方程，结合韦达定理，△F₁MH与△F₁NG的面积比，求出m的值，结合N、G坐标为(2，2

2

)、 (

1

2

，-

2

)，其中2＞xA=

3

2

，即可得出结论．

解答： 解：（Ⅰ）由y²=4x的准线为x=-1，∴|AF2|=xA+1=

5

2

，故记A(

3

2

，

6

)
又F₁（-1，0），所以2a=|AF1|+|AF2|=

7

2

+

5

2

=6，
故椭圆为

x2

9

+

y2

8

=1．…（4分）
（Ⅱ）设直线l为x=my+1（m≠0），M（x_M，y_M）、N（x_N，y_N）、G（x_G，y_G）、H（x_H，y_H）
联立

x=my+1 x2 9 + y2 8 =1

，得（8m²+9）y²+16my-64=0，…（6分）
则

yM+yH= -16m 8m2+9 yMyH= -64 8m2+9

①…（8分）
联立

x=my+1 y2=4x

，得y²-4my-4=0，则

yN+yG=4m yNyG=-4

②（10分）
△F₁MH与△F₁NG的面积比

S△F1MH

S△F1NG

=

|MH|

|NG|

=

|yM-yH|

|yN-yG|

=

(16m)2+4×64(8m2+9) 8m2+9

16m2+16

整理得

S△F1MH

S△F1NG

=

12

8m2+9

=

6

5

⇒m2=

1

8

…（12分）
若m=

2

4

，由②知N、G坐标为(2，2

2

)、 (

1

2

，-

2

)，其中2＞xA=

3

2

，故N不在“盾圆C”上；
同理m=-

2

4

也不满足，故符合题意的直线l不存在．…（14分）

点评：本题考查椭圆的标准方程，考查抛物线的定义，考查直线与椭圆、抛物线的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，有难度．