题目内容
11.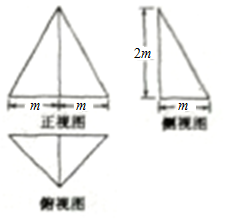 一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )| A. | $36\sqrt{3}$ | B. | $\frac{98}{3}$ | C. | $\frac{116}{3}$ | D. | $\frac{128}{3}$ |
分析 几何体是三棱锥,根据三视图知几何体的后侧面与底面垂直,高为2m,结合直观图判定外接球的球心在后侧面的高SO上,利用球心到A、S的距离相等求得半径,代入球的表面积公式计算
解答 解:由三视图知:几何体是三棱锥,如图,且几何体的后侧面SAC与底面垂直,高SO为2m,
其中OA=OB=OC=m,SO⊥平面ABC,
其外接球的球心在SO上,因为这个几何体的外接球的表面积为100π=4π×R2,解得R=5=SM,
设球心为M,OM=x,
则$\sqrt{{x}^{2}+{m}^{2}}$=5=2m-x,⇒m=4,x=3,
所以几何体S-ABC的体积为$\frac{1}{3}×\frac{1}{2}×8×4×8=\frac{128}{3}$;
故选D.
点评 本题考查三视图复原几何体形状的判断,几何体的表面积与体积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
1.平面直角坐标系中,已知点A(1,-2),B(4,0),P(a,1),N(a+1,1),当四边形PABN的周长最小时,过三点A,P,N的圆的圆心坐标是( )
| A. | (3,-$\frac{9}{8}$) | B. | (3,-$\frac{7}{8}$) | C. | (5,-$\frac{9}{8}$) | D. | (4,-$\frac{5}{8}$) |
19.已知数列{an}的前n项和记为Sn,${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,则an=( )
| A. | ${(-\frac{1}{2})^n}$ | B. | $-\frac{1}{2^n}$ | C. | $-{(-\frac{1}{2})^n}$ | D. | $-{(\frac{1}{2})^{n-1}}$ |
6.如图是某几何体的三视图,图中小方格单位长度为1,则该几何体外接球的表面积为( )

| A. | 8π | B. | 12π | C. | 16π | D. | 24π |
20.一个三棱锥的三视图如图所示,则该几何体的体积为( )


| A. | 1 | B. | $\frac{4\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 2 |
1.若函数f(x)在R上可导,f(x)=2xf'(e)+lnx,则f'(e)=( )
| A. | 1 | B. | -1 | C. | $-\frac{1}{e}$ | D. | -e |