题目内容
1．若函数f（x）在R上可导，f（x）=2xf'（e）+lnx，则f'（e）=（ ）| A． | 1 | B． | -1 | C． | $-\frac{1}{e}$ | D． | -e |
分析 利用求导法则求出f（x）的导函数，把x=e代入导函数中得到关于f′（e）的方程，求出方程的解即可得到f′（e）的值．
解答 解：求导得：f′（x）=2f'（e）+$\frac{1}{x}$，
把x=e代入得：f′（e）=$\frac{1}{e}$+2f′（e），
解得：f′（e）=-$\frac{1}{e}$，
故选：C
点评 本题要求学生掌握求导法则．学生在求f（x）的导函数时注意f′（e）是一个常数，这是本题的易错点．
练习册系列答案
名校课堂系列答案
相关题目
11．
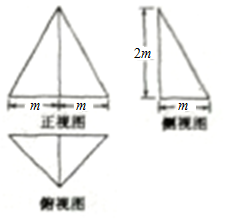一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）
一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）| A． | $36\sqrt{3}$ | B． | $\frac{98}{3}$ | C． | $\frac{116}{3}$ | D． | $\frac{128}{3}$ |
6．设f（x）是定义在正整数集上的函数，且f（x）满足：“当f（k）＞k2成立时，总可推出f（k+1）＞（k+1）2成立”．那么，下列命题总成立的是（ ）
| A． | 若f（1）≤1成立，则f（9）≤81成立 | |
| B． | 若f（2）≤4成立，则f（1）＞1成立 | |
| C． | 若f（3）＞9成立，则当k≥1时，均有f（k）＞k2成立 | |
| D． | 若f（3）＞16成立，则当k≥3时，均有f（k）＞k2成立 |