题目内容
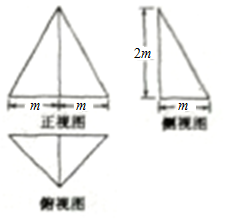
6．如图是某几何体的三视图，图中小方格单位长度为1，则该几何体外接球的表面积为（ ）
| A． | 8π | B． | 12π | C． | 16π | D． | 24π |
分析 根据三视图可知该几何体为四棱锥的一半，即三棱锥，且对应四棱锥的一条侧棱与底面垂直，把四棱锥补成长方体，则长方体的长宽高分别为2，2，4，利用CFT 的对角线为外接球的直径求外接球的半径，代入球的表面积公式计算
解答 
解：由三视图知：几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，如图
把四棱锥补成长方体，则长方体的长宽高分别为2，2，4，
∴长方体的外接球就是三棱锥的外接球，
所以外接球的直径为长方体的体对角线长度为$\sqrt{{2}^{2}+{2}^{2}+{4}^{2}}=\sqrt{24}=2\sqrt{6}$，
所以半径为$\sqrt{6}$，所以外接球的表面积为$4π（\sqrt{6}）^{2}=24π$；
故选D．
点评 本题考查了由三视图求几何体的外接球的表面积，判断几何体的几何特征，是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
11．
一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）
一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）| A． | $36\sqrt{3}$ | B． | $\frac{98}{3}$ | C． | $\frac{116}{3}$ | D． | $\frac{128}{3}$ |
18．下列函数中，最小值是2的是（ ）
| A． | y=x+$\frac{1}{x}$ | B． | y=sinx+$\frac{1}{sinx}$（0$＜x＜\frac{π}{2}$） | ||
| C． | y=lgx+$\frac{1}{lgx}$（1＜x＜10） | D． | y=x+$\frac{2}{\sqrt{x}}$-1 |
15．在△ABC中，$A=\frac{π}{3}$，$a=\sqrt{3}$，$b=\sqrt{2}$，则C=（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{7π}{12}$ | D． | $\frac{5π}{12}$ |