题目内容
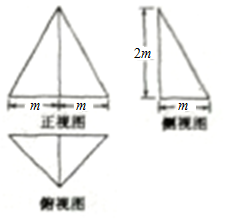
20．一个三棱锥的三视图如图所示，则该几何体的体积为（ ）
| A． | 1 | B． | $\frac{4\sqrt{3}}{3}$ | C． | $\frac{8\sqrt{3}}{3}$ | D． | 2 |
分析 由三视图可得到如图所示几何体，该几何体是由正方体切割得到的，三棱锥的高为$\sqrt{3}$，可得几何体的体积．
解答 
解：由三视图可得到如图所示几何体，该几何体是由正方体切割得到的，
三棱锥的高为$\sqrt{3}$，
∴该几何体的体积为$\frac{1}{3}$×$\frac{\sqrt{3}}{4}×（2\sqrt{2}）^{2}×\sqrt{3}$=2．
故选D．
点评 本题考查由三视图求几何体的体积，考查空间想象能力，计算能力，属于中档题．
练习册系列答案
综合自测系列答案
相关题目
11．
一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）
一个几何体的正视图、侧视图和俯视图如图所示，若这个几何体的外接球的表面积为100π，则该几何体的体积为（ ）| A． | $36\sqrt{3}$ | B． | $\frac{98}{3}$ | C． | $\frac{116}{3}$ | D． | $\frac{128}{3}$ |
8．在等差数列{an}中，a3+a8=-3，那么S10等于（ ）
| A． | -9 | B． | -11 | C． | -13 | D． | -15 |
15．在△ABC中，$A=\frac{π}{3}$，$a=\sqrt{3}$，$b=\sqrt{2}$，则C=（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{7π}{12}$ | D． | $\frac{5π}{12}$ |
5．若实数x，y，m，n满足x2+y2=a，m2+n2=b，则mx+ny的最大值为（ ）
| A． | $\frac{a+b}{2}$ | B． | $\sqrt{ab}$ | C． | $\sqrt{\frac{{{a^2}+{b^2}}}{2}}$ | D． | $\frac{ab}{a+b}$ |