题目内容
19.已知数列{an}的前n项和记为Sn,${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,则an=( )| A. | ${(-\frac{1}{2})^n}$ | B. | $-\frac{1}{2^n}$ | C. | $-{(-\frac{1}{2})^n}$ | D. | $-{(\frac{1}{2})^{n-1}}$ |
分析 ${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,n≥2时,an=Sn-Sn-1,化为:an=-$\frac{1}{2}{a}_{n-1}$.n=1时,a1=S1=$\frac{1}{3}({a}_{1}-1)$,解得a1.利用等比数列的通项公式即可得出.
解答 解:∵${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,
∴n≥2时,an=Sn-Sn-1=$\frac{1}{3}({a}_{n}-1)$-$\frac{1}{3}({a}_{n-1}-1)$,化为:an=-$\frac{1}{2}{a}_{n-1}$.
n=1时,a1=S1=$\frac{1}{3}({a}_{1}-1)$,解得a1=$-\frac{1}{2}$.
∴数列{an}是等比数列,首项与公比都为-$\frac{1}{2}$.
则an=$(-\frac{1}{2})^{n}$.
故选:A.
点评 本题考查了等比数列的定义通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.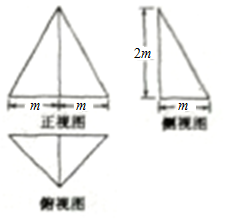 一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
 一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )| A. | $36\sqrt{3}$ | B. | $\frac{98}{3}$ | C. | $\frac{116}{3}$ | D. | $\frac{128}{3}$ |
8.在等差数列{an}中,a3+a8=-3,那么S10等于( )
| A. | -9 | B. | -11 | C. | -13 | D. | -15 |