题目内容
已知f(x)=cos2x-sin2x.
(1)求f(
)的值及f(x)的最大值;
(2)求f(x)的递增区间.
(1)求f(
| π |
| 3 |
(2)求f(x)的递增区间.
考点:二倍角的余弦,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)由条件利用二倍角的余弦公式求得f(x)=cos2x,从而求得f(
)的值及f(x)的最大值.
(2)令2kπ-π≤2x≤2kπ,k∈z,求得x的范围,可得f(x)的递增区间.
| π |
| 3 |
(2)令2kπ-π≤2x≤2kπ,k∈z,求得x的范围,可得f(x)的递增区间.
解答:
解:(1)∵f(x)=cos2x-sin2x=cos2x,
∴f(
)=cos
π=-
,且fmax(x)=1.
(2)令2kπ-π≤2x≤2kπ,k∈z,求得 kπ-
≤x≤kπ,k∈z,
故f(x)的递增区间为[kπ-
,kπ],其中k∈Z.
∴f(
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
(2)令2kπ-π≤2x≤2kπ,k∈z,求得 kπ-
| π |
| 2 |
故f(x)的递增区间为[kπ-
| π |
| 2 |
点评:本题主要考查二倍角的余弦公式、余弦函数的增区间,属于基础题.

练习册系列答案
相关题目
sin5°sin25°-sin95°sin65°的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
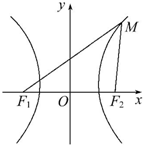 如图,设有双曲线
如图,设有双曲线