题目内容
已知奇函数y=f(x)定义在[-1,1]上,且在定义域内是减函数,若f(a2-a-1)+f(4a-5)>0,求实数a的取值范围.
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:将f(a2-a-1)+f(4a-5)>0变为f(a2-a-1)>-f(4a-5),利用奇函数,变为f(a2-a-1)>f(-4a+5),再由单调性转化为直接关于a的不等式求解即可.
解答:
解:因为f(a2-a-1)+f(4a-5)>0,所以f(a2-a-1)>-f(4a-5),
因为函数y=f(x)是奇函数,所以上式变为f(a2-a-1)>f(-4a+5),
又因为定义在[-1,1]上的函数y=f(x)是减函数,所以
解得:1≤a≤
.
因为函数y=f(x)是奇函数,所以上式变为f(a2-a-1)>f(-4a+5),
又因为定义在[-1,1]上的函数y=f(x)是减函数,所以
|
解得:1≤a≤
-3+
| ||
| 2 |
点评:本题考查的知识点是奇偶性与单调性的综合,函数的单调性的性质,其中利用函数的性质,将原不等式转化为一个关于a的不等式组,是解答本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
“所有9的倍数都是3的倍数.某数是9的倍数,故该数为3的倍数,”上述推理( )
| A、完全正确 |
| B、推理形式不正确 |
| C、错误,因为大小前提不一致 |
| D、错误,因为大前提错误 |
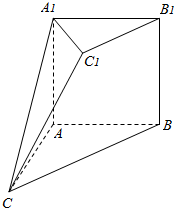 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=