题目内容
(1)已知复数(m2-5m+6)+(m2-3m)i是纯虚数,求实数m的值;
(2)把复数z的共轭复数记做
,已知(1+2i)
=4+3i,求z及
.
(2)把复数z的共轭复数记做
. |
| z |
. |
| z |
| z | ||
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:(1)由纯虚数定义得
,由此能求出m的值.
(2)设z=a+bi,由(1+2i)
=4+3i,得(1+2i)(a+bi)=4+3i,由此能求出z=2-i,
=
=
-
i.
|
(2)设z=a+bi,由(1+2i)
. |
| z |
| z | ||
|
| 2-i |
| 2+i |
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:(1)∵复数(m2-5m+6)+(m2-3m)i是纯虚数,
∴
,解得m=2.
(2)设z=a+bi,则
=a-bi,
∵(1+2i)
=4+3i,
∴(1+2i)(a+bi)=4+3i,
∴a+2ai+bi+2bi2
=(a-2b)+(2a+b)i
=4+3i,
∴
,解得a=2,b=-1,
∴z=2-i,
∴
=
=
=
=
-
i.
∴
|
(2)设z=a+bi,则
. |
| z |
∵(1+2i)
. |
| z |
∴(1+2i)(a+bi)=4+3i,
∴a+2ai+bi+2bi2
=(a-2b)+(2a+b)i
=4+3i,
∴
|
∴z=2-i,
∴
| z | ||
|
| 2-i |
| 2+i |
| (2-i)(2-i) |
| (2+i)(2-i) |
=
| 4-4i+i2 |
| 4-i2 |
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题考查实数的求法,考查复数的代数形式的乘除运算,解题时要认真审题,是基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
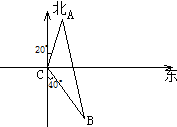 如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )| A、1km | ||
B、
| ||
C、
| ||
| D、2km |
若球的表面积扩大到原来的2倍,则球的体积扩大到原来的( )
| A、2倍; | ||
B、
| ||
C、2
| ||
D、3
|
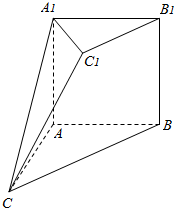 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=