题目内容
已知函数f(x)满足f(x)=2f(
),当x∈[1,+∞)时,f(x)=lnx,若在区间(0,e2)内,函数g(x)=f(x)-ax与x轴有3个不同的交点,则实数a的取值范围是 .
| 1 |
| x |
考点:抽象函数及其应用,根的存在性及根的个数判断
专题:计算题,作图题,导数的综合应用
分析:由题意可得f(x)=
;从而在区间(0,e2)内,a=
=
;结合函数图象求解.
|
| f(x) |
| x |
|
解答:
解:由题意,当0<x<1时,
f(x)=2f(
)=2ln
=-2lnx,
故f(x)=
;
在区间(0,e2)内,函数g(x)=f(x)-ax与x轴有3个不同的交点,
即在区间(0,e2)内,f(x)-ax=0有3个不同的解,
即在区间(0,e2)内,
a=
=
;
作函数y=
的图象如下,
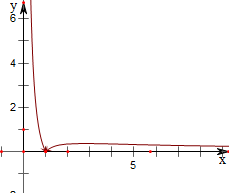
结合图象可得,当x∈(1,e2)时,
令y′=
=0得,
x=e;
故y(e)=
;y(e2)=
;
故实数a的取值范围是(
,
).
故答案为:(
,
).
f(x)=2f(
| 1 |
| x |
| 1 |
| x |
故f(x)=
|
在区间(0,e2)内,函数g(x)=f(x)-ax与x轴有3个不同的交点,
即在区间(0,e2)内,f(x)-ax=0有3个不同的解,
即在区间(0,e2)内,
a=
| f(x) |
| x |
|
作函数y=
| f(x) |
| x |

结合图象可得,当x∈(1,e2)时,
令y′=
| 1-lnx |
| x2 |
x=e;
故y(e)=
| 1 |
| e |
| 2 |
| e2 |
故实数a的取值范围是(
| 2 |
| e2 |
| 1 |
| e |
故答案为:(
| 2 |
| e2 |
| 1 |
| e |
点评:本题考查了导数的应用及学生作图的能力,属于中档题.

练习册系列答案
相关题目
已知命题p:?m∈R,m+1≤0,命题q:?x∈R,x2+mx+1>0.若“p∧q”为假命题,则实数m的取值范围是( )
| A、(-∞,-2]∪(-1,+∞) |
| B、[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,2] |