题目内容
与抛物线y2=8x相切且倾斜角为135°的直线l与x轴和y轴的交点分别是A和B,那么过A,B两点的最小圆截抛物线y2=8x的准线所得的弦长为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知设出直线l的方程y=-x+m,联立直线方程和抛物线方程,化为关于x的一元二次方程,由判别式等于0求出m的值,得到直线方程,求出A,B的坐标,得到以AB为直径的最小圆的方程,和抛物线的准线联立即可求得弦长.
解答:
解:如图,
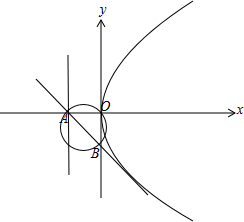
设与抛物线y2=8x相切且倾斜角为135°的直线l的方程为y=-x+m,
联立
,得x2-(2m+8)x+m2=0,
由△=(2m+8)2-4m2=0,解得:m=-2.
∴准线l的方程为y=-x-2.
∴直线l与x轴和y轴的交点A(-2,0)和B(0,-2).
则过A,B两点的最小圆的方程为:(x+1)2+(y+1)2=2.
∵抛物线y2=8x的准线方程为x=-2,
代入圆(x+1)2+(y+1)2=2,得y=0或y=-2.
∴过A,B两点的最小圆截抛物线y2=8x的准线所得的弦长为0-(-2)=2.
故答案为:2.

设与抛物线y2=8x相切且倾斜角为135°的直线l的方程为y=-x+m,
联立
|
由△=(2m+8)2-4m2=0,解得:m=-2.
∴准线l的方程为y=-x-2.
∴直线l与x轴和y轴的交点A(-2,0)和B(0,-2).
则过A,B两点的最小圆的方程为:(x+1)2+(y+1)2=2.
∵抛物线y2=8x的准线方程为x=-2,
代入圆(x+1)2+(y+1)2=2,得y=0或y=-2.
∴过A,B两点的最小圆截抛物线y2=8x的准线所得的弦长为0-(-2)=2.
故答案为:2.
点评:本题考查了抛物线的简单几何性质,考查了直线与圆锥曲线的关系,求出过A,B两点的最小圆的方程是解答该题的关键,是中档题.

练习册系列答案
相关题目
