题目内容
1．若直线ax+by+1=0（a、b＞1）过圆x2+y2+8x+2y+1=0的圆心，则$\frac{1}{a}+\frac{4}{b}$的最小值为（ ）| A． | 8 | B． | 12 | C． | 16 | D． | 20 |
分析 求出圆的圆心坐标，代入直线方程，得到1=4a+b的关系式，然后通过”1“的代换利用基本不等式求解即可．
解答 解：圆x2+y2+8x+2y+1=0的圆心（-4，-1）在直线ax+by+1=0上，
所以-4a-b+1=0，即 1=4a+b代入，
得 $\frac{1}{a}+\frac{4}{b}$=（$\frac{1}{a}+\frac{4}{b}$）（4a+b）=8+$\frac{b}{a}$+$\frac{16a}{b}$≥16（a＞0，b＞0当且仅当4a=b时取等号）
则$\frac{1}{a}+\frac{4}{b}$的最小值为16，
故选C．
点评 本题考查直线与圆的位置关系的应用，基本不等式求解函数的最值，考查转化思想以及计算能力．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11．记数列{an}的前n项和为Sn，若Sn=3an+1，则a10=（ ）
| A． | -$\frac{{3}^{9}}{{2}^{10}}$ | B． | -$\frac{{3}^{10}}{{2}^{10}}$ | C． | $\frac{{3}^{9}}{{2}^{10}}$ | D． | $\frac{{3}^{10}}{{2}^{10}}$ |
12．过点M（2，-2p）作抛物线x2=2py（p＞0）的两条切线，切点分别为A，B，若线段AB中点的纵坐标为6，则抛物线的方程为（ ）
| A． | x2=2y | B． | x2=4y | C． | x2=2y或x2=4y | D． | x2=3y或x2=2y |
16．设偶函数f（x）满足f（x）=log4（x+2）-1（x≥0），则{x|f（x-2）＞0}等于（ ）
| A． | {x|x＜-2或x＞4} | B． | {x|x＜0或x＞4} | C． | {x|x＜0或x＞6} | D． | {x|x＜-2或x＞2} |
13．若曲线y=x2+ax+b在点（0，b）处的切线方程是3x-y+1=0，则（ ）
| A． | a=-3，b=1 | B． | a=3，b=1 | C． | a=-3，b=-1 | D． | a=3，b=-1 |
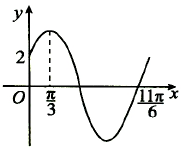已知函数$f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜\frac{π}{2}）$的部分图象如图所示．