题目内容
过双曲线
-x2=1上任一点P向两渐近线做垂线，垂足分别为A、B，则|AB|的最小值为 ．
| y2 |
| 3 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意，P，A，B，O四点共圆，求|AB|的最小值，只需要求出圆的直径的最小值．
解答：
解：由题意，P，A，B，O四点共圆，求|AB|的最小值，只需要求出圆的直径的最小值，显然为
，
∵
-x2=1的渐近线为
-x2=0，
∴∠AOB=120°，
∴
=
，
∴|AB|=1.5，
故答案为：1.5．
| 3 |
∵
| y2 |
| 3 |
| y2 |
| 3 |
∴∠AOB=120°，
∴
| |AB| |
| sin120° |
| 3 |
∴|AB|=1.5，
故答案为：1.5．
点评：本题考查双曲线的性质，考查正弦定理的运用，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
如图，PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD为直角梯形，且AB∥CD，BC⊥AB，BC=CD=BO=PO，EA=AO=
如图是长和宽分别相等的两个矩形，给定下列四个命题：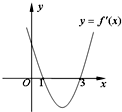
已知函数f（x）=x3+ax2+bx+c的导函数y=f′（x）的图象如图所示，给出下列三个结论：
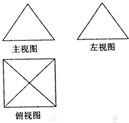一个几何体的三视图如图所示，其中主（正）视图是边长为2的正三角形，俯视图是正方形，那么该几何体的左（侧）视图的面积是（ ）
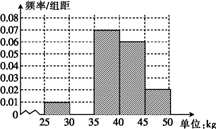某养猪厂计划将重量为25kg到50kg的10000头猪向外出售，现从中随机抽取了100头猪进行称重，已知这些猪的重量的频率分布表及不完整的频率分布直方图（如图）．