题目内容
已知函数f(x)=|x-3|+|x-2|+k.
(1)若f(x)≥3恒成立,求k的取值范围;
(2)当k=1时,解不等式:f(x)<3x.
(1)若f(x)≥3恒成立,求k的取值范围;
(2)当k=1时,解不等式:f(x)<3x.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)根据 f(x)=|x-3|+|x-2|≥3-k,利用绝对值三角不等式求出左侧最小值,从而求得不等式f(x)≥3成立的k的取值范围.
(2)由|x-3|+|x-2|<3x-1,通过去掉绝对值符号,解答不等式求出解集即可.
(2)由|x-3|+|x-2|<3x-1,通过去掉绝对值符号,解答不等式求出解集即可.
解答:
解:(1)∵f(x)=|x-3|+|x-2|+k,f(x)≥3恒成立,即(|x-3|+|x-2|)min≥3-k,
|x-3|+|x-2|≥|x-3-x+2|=1,
∴(|x-3|+|x-2|)min=1,可得1≥3-k,解得k≥2,
使得不等式f(x)≥3恒成立的k的取值范围是[2,+∞).
(2)当x≤2时,不等式化为:5x>6,解得x>
,可得
<x≤2.
当2<x<3时,不等式化为:3x>2,解得x>
,可得2<x<3.
当x≥3时,不等式化为:x>-4,解得x≥3.
综上不等式的解集为:(
,+∞)
|x-3|+|x-2|≥|x-3-x+2|=1,
∴(|x-3|+|x-2|)min=1,可得1≥3-k,解得k≥2,
使得不等式f(x)≥3恒成立的k的取值范围是[2,+∞).
(2)当x≤2时,不等式化为:5x>6,解得x>
| 6 |
| 5 |
| 6 |
| 5 |
当2<x<3时,不等式化为:3x>2,解得x>
| 2 |
| 3 |
当x≥3时,不等式化为:x>-4,解得x≥3.
综上不等式的解集为:(
| 6 |
| 5 |
点评:本题主要考查绝对值不等式的性质,绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
设全集U={x|0<x<2},集合A={x|0<x≤1},则集合∁UA=( )
| A、(0,1) |
| B、(0,1] |
| C、(1,2) |
| D、[1,2) |
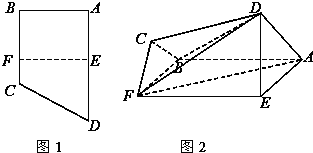 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.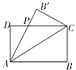 某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为
某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为