题目内容
调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表：
（参考数据和公式见卷首）你认为婴儿的性别与出生时间有关系的把握为（ ）
| 晚上 | 白天 | 合计 | |
| 男婴 | 50 | 25 | 75 |
| 女婴 | 10 | 15 | 25 |
| 合计 | 60 | 40 | 100 |
| A、80% | B、90% |
| C、95% | D、97.5% |
考点：独立性检验的应用
专题：计算题,概率与统计
分析：根据所给的数据，代入求观测值的公式，得到观测值，把观测值同临界值进行比较得到结论．
解答：
解：根据所给的数据代入求观测值的公式，得到
k2=
≈5.556＞5.024，
∴有97.5%的把握认为婴儿的性别与出生时间有关系．
故选D．
k2=
| 100•(50•15-25•10)2 |
| 60•40•75•25 |
∴有97.5%的把握认为婴儿的性别与出生时间有关系．
故选D．
点评：本题考查独立性检验的应用，本题解题的关键是理解临界值对应的概率的意义，能够看出两个变量之间的关系，属于基础题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
对于函数f（x），若存在区间[m，n]（m＜n），使得f（x）在区间[m，n]上的值域为[λm，λn]，则称f（x）为“λ倍函数”，若f（x）=ax（a＞1）为“1倍函数”，则a的取值范围为（ ）
A、（1，
| ||
B、（
| ||
C、（1，e
| ||
D、（e
|
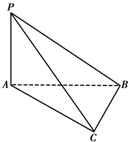如图所示，已知PA垂直于△ABC所在平面，且∠ACB=90°，连结PB、PC，则图形中互相垂直的平面有（ ）| A、一对 | B、两对 | C、三对 | D、四对 |
下列关于独立性检验的说法中，错误的是（ ）
| A、独立性检验得到的结论一定正确 |
| B、独立性检验依赖小概率原理 |
| C、样本不同，独立性检验的结论可能有差异 |
| D、独立性检验不是判定两事物是否相关的唯一方法 |
如图程序运行结果为（ ）
| A、3 | B、4 | C、5 | D、6 |