题目内容
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如表.预计在今后的销售中,销量与单价仍然服从
=bx+a( b=-20,a=
-b
)的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元.
 |
| y |
. |
| y |
. |
| x |
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
A、
| ||
| B、8 | ||
C、
| ||
D、
|
考点:回归分析
专题:计算题,概率与统计
分析:计算平均数,利用b=-20,a=
-b
,求得回归直线方程,设工厂获得的利润为L元,利用利润=销售收入-成本,建立函数,利用配方法可求工厂获得的利润最大.
. |
| y |
. |
| x |
解答:
解:
=
(8+8.2+8.4+8.6+8.8+9)=8.5,
=
(90+84+83+80+75+68)=80,
∵b=-20,a=
-b
,
∴a=80+20×8.5=250,
∴回归直线方程
=-20x+250;
设工厂获得的利润为L元,则L=x(-20x+250)-4(-20x+250)=-20(x-
)2+361.25
∴该产品的单价应定为
元,工厂获得的利润最大.
故选:C.
. |
| x |
| 1 |
| 6 |
. |
| y |
| 1 |
| 6 |
∵b=-20,a=
. |
| y |
. |
| x |
∴a=80+20×8.5=250,
∴回归直线方程
 |
| y |
设工厂获得的利润为L元,则L=x(-20x+250)-4(-20x+250)=-20(x-
| 33 |
| 4 |
∴该产品的单价应定为
| 33 |
| 4 |
故选:C.
点评:本题主要考查回归分析,考查二次函数,考查运算能力、应用意识,属于中档题.

练习册系列答案
相关题目
在极坐标系中,直线ρsin(θ+
)=2,被圆ρ=3截得的弦长为( )
| π |
| 4 |
A、2
| ||
| B、2 | ||
C、2
| ||
D、2
|
对于函数f(x),若存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[λm,λn],则称f(x)为“λ倍函数”,若f(x)=ax(a>1)为“1倍函数”,则a的取值范围为( )
A、(1,
| ||
B、(
| ||
C、(1,e
| ||
D、(e
|
把函数y=sin3x的图象适当变化就可以得到y=
(sin3x-cos3x)的图象,这个变化可以是( )
| ||
| 2 |
A、沿x轴方向向右平移
| ||
B、沿x轴方向向左平移
| ||
C、沿x轴方向向右平移
| ||
D、沿x轴方向向左平移
|
已知点F1,F2分别是椭圆
+
=1(a>b>0)的左、右焦点,点P是椭圆上的一个动点,若使得满足△PF1F2是直角三角形的动点P恰好有6个,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=|x+2|-|x-1|,则f(x)的值域是( )
| A、(-3,3) |
| B、[-3,3] |
| C、[3,+∞) |
| D、[-3,+∞) |
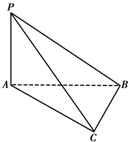 如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )
如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )| A、一对 | B、两对 | C、三对 | D、四对 |