题目内容
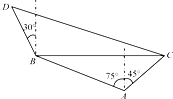 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(| 3 |
| 3 |
考点:余弦定理的应用
专题:解三角形
分析:设缉私船追上走私船需t小时,进而可表示出CD和BD,进而在△ABC中利用余弦定理求得BC,进而在△BCD中,根据正弦定理可求得sin∠BCD的值,即可得到缉私船沿什么方向能最快追上走私船.
解答:
解:设缉私船追上走私船需t小时,则有CD=10
t,BD=10t.
在△ABC中,
∵AB=2,AC=
-1,∠BAC=45°+75°=120°.
根据余弦定理BC2=AB2+AC2-2AB•ACcos∠BAC=6可求得BC=
.
∴sin∠ACB=
=
,∴∠ACB=45°,∴BC与正北方向垂直,
∵∠CBD=90°+30°=120°.
在△BCD中,根据正弦定理可得
sin∠BCD=
=
=
,
∴∠BCD=30°
∴缉私船沿北偏西60°方向能最快追上走私船.
| 3 |
在△ABC中,
∵AB=2,AC=
| 3 |
根据余弦定理BC2=AB2+AC2-2AB•ACcos∠BAC=6可求得BC=
| 6 |
∴sin∠ACB=
| ABsin∠BAC |
| BC |
| ||
| 2 |
∵∠CBD=90°+30°=120°.
在△BCD中,根据正弦定理可得
sin∠BCD=
| BD•sin∠CBD |
| CD |
| 10t•sin120° | ||
10
|
| 1 |
| 2 |
∴∠BCD=30°
∴缉私船沿北偏西60°方向能最快追上走私船.
点评:本题主要考查了解三角形的实际应用.考查了运用三角函数的基础知识解决实际的问题.

练习册系列答案
相关题目
收集一只棉铃虫的产卵数y与温度X的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y与X之间的回归方程,算出对应相关指数R2如下表:
则这组数据模型的回归方程的最好选择应是( )
则这组数据模型的回归方程的最好选择应是( )
| 拟合曲线 | 直 线 | 指数曲线 | 抛 物 线 | 二次曲线 | ||||||||||
| y与x回归方程 |
|
|
|
| ||||||||||
| 相关指数R2 | 0.746 | 0.996 | 0.902 | 0.002 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4,
如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4, 如图,在直三棱柱(侧棱和底面垂直的棱柱)ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.
如图,在直三棱柱(侧棱和底面垂直的棱柱)ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.