题目内容
已知椭圆C:
+
=1(a>b>0)的焦距为2
,且过点A(
,
).
(Ⅰ)求椭圆的方程;
(Ⅱ)已知l:y=kx-1,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)已知l:y=kx-1,是否存在k使得点A关于l的对称点B(不同于点A)在椭圆C上?若存在求出此时直线l的方程,若不存在说明理由.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)通过椭圆的焦距求出c,利用a、b、c的关系以及点的坐标适合椭圆方程,求出a,b,即可求椭圆的方程;
(Ⅱ)法1:当k=0时,验证点B(
,-
)不在椭圆上;当k≠0时,可设直线AB:y=-
(x-
)+
,代入
+y2=1利用韦达定理,以及对称综上,说明不存在k满足条件.
法2:设AB:x=-ky+m,代入椭圆方程
+y2=1利用韦达定理,以及对称知识,说明k=1,导出对称点B与点A重合,不合题意,不存在k满足条件.
法3:由l:y=kx-1可知直线l恒过点P(0,-1),设点A关于l的对称点B坐标为(x0,y0),
利用|PA|=|PB|,求出B(-
,
)与A关于x=0对称,不存在k满足条件.
(Ⅱ)法1:当k=0时,验证点B(
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| k |
| 3 |
| 2 |
| 1 |
| 2 |
| x2 |
| 3 |
法2:设AB:x=-ky+m,代入椭圆方程
| x2 |
| 3 |
法3:由l:y=kx-1可知直线l恒过点P(0,-1),设点A关于l的对称点B坐标为(x0,y0),
利用|PA|=|PB|,求出B(-
| 3 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)椭圆C:
+
=1(a>b>0)的焦距为2
,∴c=
,则a2-b2=2…①,
椭圆过点A(
,
).
+
=1…②,解①②可得a2=3,b2=1,
∴椭圆的方程:
+y2=1
(Ⅱ)法1:当k=0时,直线l:y=-1,点B(
,-
)不在椭圆上;
当k≠0时,可设直线AB:y=-
(x-
)+
,即2x+2ky-3-k=0
代入
+y2=1整理得(4k2+12)y2-4k(k+3)y+(k+3)2-12=0
因为y1+y2=
,
所以x1+x2=(k+3)-(ky1+ky2)=k+3-
=
若A,B关于直线l对称,
则其中点(
,
)在直线y=kx-1上
所以
=
-1,解得k=1
因为此时点A(
,
)在直线l上,
所以对称点B与点A重合,不合题意
所以不存在k满足条件.
法2:设AB:x=-ky+m,代入椭圆方程
+y2=1化简得(k2+3)y2-2kmy+m2-3=0,yA+yB=
,所以xA+xB=-
+2m=
若A,B关于直线l对称,则其中点(
,
)在直线y=kx-1上,
所以
=
-1,即2km=k2+3.
又A(
,
)在直线AB:x=-ky+m上,
所以2m-k=3,
消m得(3+k)k=k2+3,所以k=1
因为此时点A(
,
)在直线l上,
所以对称点B与点A重合,不合题意,
所以不存在k满足条件.
法3:由l:y=kx-1可知直线l恒过点P(0,-1),
设点A关于l的对称点B坐标为(x0,y0),
因为点A,B关于l对称,所以|PA|=|PB|
所以x02+(y0+1)2=
①
又B在椭圆上,所以
+y02=1②
联立①②解得
或
因为B(
,
)与A点重合,舍,
因为B(-
,
)与A关于x=0对称
所以不存在k满足条件.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
椭圆过点A(
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4a2 |
| 1 |
| 4b2 |
∴椭圆的方程:
| x2 |
| 3 |
(Ⅱ)法1:当k=0时,直线l:y=-1,点B(
| 3 |
| 2 |
| 5 |
| 2 |
当k≠0时,可设直线AB:y=-
| 1 |
| k |
| 3 |
| 2 |
| 1 |
| 2 |
代入
| x2 |
| 3 |
因为y1+y2=
| 4k(k+3) |
| 4k2+12 |
所以x1+x2=(k+3)-(ky1+ky2)=k+3-
| 4k2(k+3) |
| 4k2+12 |
| 12(k+3) |
| 4k2+12 |
若A,B关于直线l对称,
则其中点(
| 6(k+3) |
| 4k2+12 |
| 2k(k+3) |
| 4k2+12 |
所以
| 2k(k+3) |
| 4k2+12 |
| 6k(k+3) |
| 4k2+12 |
因为此时点A(
| 3 |
| 2 |
| 1 |
| 2 |
所以对称点B与点A重合,不合题意
所以不存在k满足条件.
法2:设AB:x=-ky+m,代入椭圆方程
| x2 |
| 3 |
| 2km |
| k2+3 |
| 2k2m |
| k2+3 |
| 6m |
| k2+3 |
若A,B关于直线l对称,则其中点(
| 3m |
| k2+3 |
| km |
| k2+3 |
所以
| km |
| k2+3 |
| 3km |
| k2+3 |
又A(
| 3 |
| 2 |
| 1 |
| 2 |
所以2m-k=3,
消m得(3+k)k=k2+3,所以k=1
因为此时点A(
| 3 |
| 2 |
| 1 |
| 2 |
所以对称点B与点A重合,不合题意,
所以不存在k满足条件.
法3:由l:y=kx-1可知直线l恒过点P(0,-1),
设点A关于l的对称点B坐标为(x0,y0),
因为点A,B关于l对称,所以|PA|=|PB|
所以x02+(y0+1)2=
| 9 |
| 2 |
又B在椭圆上,所以
| x02 |
| 3 |
联立①②解得
|
|
因为B(
| 3 |
| 2 |
| 1 |
| 2 |
因为B(-
| 3 |
| 2 |
| 1 |
| 2 |
所以不存在k满足条件.
点评:本题考查椭圆方程的求法,直线与椭圆的对称关系的应用,考查直线与圆锥曲线的位置关系.

练习册系列答案
相关题目
若将6本不同书放到5个不同盒子里,有多少种不同放法( )
A、
| ||
B、
| ||
| C、56 | ||
| D、65 |
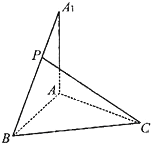 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.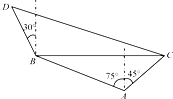 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离( 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6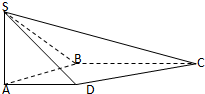 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,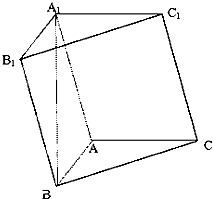 在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.
在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.