题目内容
如图，在直三棱柱（侧棱和底面垂直的棱柱）ABC-A1B1C1中，AB=AC=AA1=3a，BC=2a，D是BC的中点，F是CC1上一点，且CF=2a．（Ⅰ）求证：B1F⊥平面ADF；
（Ⅱ）求二面角F-AD-C的正切值；
（Ⅲ）试在AA1上找一点E，使得BE∥平面ADF，并说明理由．
考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题：综合题,空间位置关系与距离,空间角
分析：（I）证明B1F⊥平面ADF，只需证明B1F⊥AF，AD⊥B1F；
（Ⅱ）证明∠CDF为二面角F-AD-C的平面角，即可求出求二面角F-AD-C的正切值；
（Ⅲ）当AE=2a时，BE∥平面ADF，再进行证明即可．
（Ⅱ）证明∠CDF为二面角F-AD-C的平面角，即可求出求二面角F-AD-C的正切值；
（Ⅲ）当AE=2a时，BE∥平面ADF，再进行证明即可．
解答：
（I）证明：由ABC-A1B1C1为直三棱柱和CF=2a，AB=AC=AA1=3a，BC=2a，得B1F=
=
a，AF=
=
a，
AB1=
=
a，得AB12=AF2+B1F2
所以B1F⊥AF，…（2分）
由CC1⊥面ABC，AD?面ABC，得CC1⊥AD，
由AB=AC及D是BC的中点得：AD⊥BC，
而CC1⊥AD，BC∩CC1=C，
所以AD⊥面BCC1B1，
又BF1?面BCC1B1，
所以AD⊥B1F…（2分）
又B1F⊥AF，AF∩AD=A，
所以B1F⊥平面ADF；…（5分）
（Ⅱ）解：由（I）AD⊥面BCC1B1，而CD?面BCC1B1、DF?面BCC1B1，
所以AD⊥CD、AD⊥DF
所以∠CDF为二面角F-AD-C的平面角 …（8分）
由直三棱柱可知：∠DCF为直角，所以tan∠CDF=
=
=2…（10分）
（Ⅲ）解：当AE=2a时，BE∥平面ADF，
证明如下：连结EF、EC交AF于点M，
由AE=2a=CF，及AE∥CF可得：四边形ACFE为平行四边形．
所以M为EC中点，
又D是BC的中点，
所以BE∥DM，…（13分）
又BE?平面ADF，DM?平面ADF
所以BE∥平面ADF，命题得证． …（14分）
（I）证明：由ABC-A1B1C1为直三棱柱和CF=2a，AB=AC=AA1=3a，BC=2a，得B1F=| B1C12+C1F2 |
| 5 |
| AC2+CF2 |
| 13 |
AB1=
| AB2+BB12 |
| 18 |
所以B1F⊥AF，…（2分）
由CC1⊥面ABC，AD?面ABC，得CC1⊥AD，
由AB=AC及D是BC的中点得：AD⊥BC，
而CC1⊥AD，BC∩CC1=C，
所以AD⊥面BCC1B1，
又BF1?面BCC1B1，
所以AD⊥B1F…（2分）
又B1F⊥AF，AF∩AD=A，
所以B1F⊥平面ADF；…（5分）
（Ⅱ）解：由（I）AD⊥面BCC1B1，而CD?面BCC1B1、DF?面BCC1B1，
所以AD⊥CD、AD⊥DF
所以∠CDF为二面角F-AD-C的平面角 …（8分）
由直三棱柱可知：∠DCF为直角，所以tan∠CDF=
| FC |
| CD |
| 2a |
| a |
（Ⅲ）解：当AE=2a时，BE∥平面ADF，
证明如下：连结EF、EC交AF于点M，
由AE=2a=CF，及AE∥CF可得：四边形ACFE为平行四边形．
所以M为EC中点，
又D是BC的中点，
所以BE∥DM，…（13分）
又BE?平面ADF，DM?平面ADF
所以BE∥平面ADF，命题得证． …（14分）
点评：本题考查线面平行、线面垂直，考查面面角，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
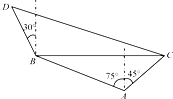在海岸A处，发现北偏西75°的方向，与A距离2海里的B处有一艘走私船，在A处北偏东45°方向，与A距离（
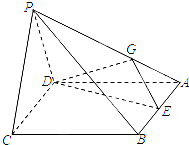如图，四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°，平面PCD⊥底面ABCD，E是AB的中点，G为PA上的一点．
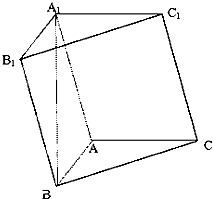在三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=A1B=2，顶点A1在底面ABC上的射影恰好为点B．