题目内容
16.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0,一个焦点与抛物线y2=-20x的焦点重合,则双曲线的方程为( )( )| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | ||
| C. | $\frac{3{x}^{2}}{25}$-$\frac{3{y}^{2}}{100}$=1 | D. | $\frac{3{x}^{2}}{100}$-$\frac{3{y}^{2}}{25}$=1 |
分析 利用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0,一个焦点与抛物线y2=-20x的焦点重合,建立方程,求出a,b,即可求出双曲线的方程.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线平行于直线x+2y+5=0,
∴$\frac{b}{a}$=$\frac{1}{2}$,
∵一个焦点与抛物线y2=-20x的焦点重合,
∴c=5,
∴a=2$\sqrt{5}$,b=$\sqrt{5}$,
∴双曲线的方程为$\frac{{x}^{2}}{20}-\frac{{y}^{2}}{5}$=1.
故选:A.
点评 本题主要考查了双曲线和抛物线的性质,属于基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.设函数f(x)=sinωx(ω>0),将f(x)的图象向左平移$\frac{π}{6}$个单位长度后,所得的图象与y=cosωx的图象重合,则ω的最小值等于( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
6.已知四面体ABCD的侧面展开图如图所示,则其体积为( )
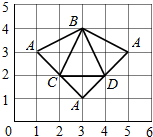

| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |

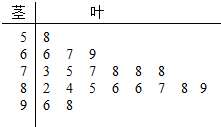 某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.
某上市公司为了解A市用户对其产品的满意度,从该市随机调查了20个用户,得到用户对其产品的满意度评分,并用茎叶图记录分数如图所示.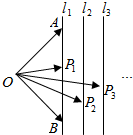 如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.
如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.